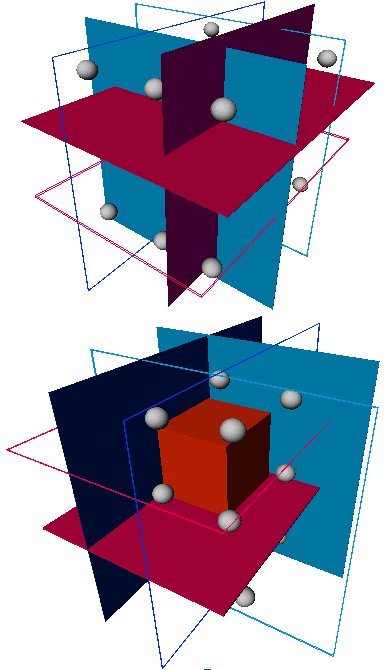Aspect Graphs


Outline

Definition
Application
Construction
Demos
References

Next

DEFINITIONS

Aspect is the topological appearance of an object. Appearance to the eye, esp, when seen from a specific view.

Viewpoint Space Partition is a partition of viewpoint space into maximal regions of constant aspect.

Event is a change in topological appearance. Represent boundaries of viewpoint space partition.

Aspect Graph is a graph with a node for every aspect and edges connecting adjacent aspects. The dual of a viewpoint space partition is an aspect graph.

Aspect graphs can be made for:

  • Convex Polyhedra
  • Non-Convex Polyhedra
  • A General Polyhedral Scene (same as non-convex polyhedra case)
  • Non-Polyhedral Objects (eg. torus)
    • Prev | Next

    APPLICATIONS

  • Computer Vision: Recognizing Polyhedra
  • Visibility Processing: Rendering Polyhedron Scenes
  • Image Based Rendering
    • An early application of aspect graphs:

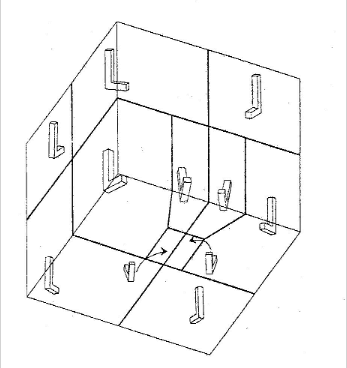
    How will an L-shaped object look from different regions of a cube?
    Prev | Next

    ASPECT GRAPHS UNDER DIFFERENT VIEWING MODELS

    Viewpoint Freedom

    Perspective Model | Orthographic Model
    More Freedom
    Viewpoint can be anywhere!    		Aspect Graph is easier!
    Viewpoint can be thought
    of as being restricted to a certain type of surface.
    What kind of surface???
    Prev | Next

    COMPUTER VISION

    Characteristic-View Approach to 3D Object Recognition

    INPUT

    SAMPLE CHARACTERISTIC VIEWS


    Top
    Bottom Left
    Top Left

    Front
    Bottom

    Basic Idea

    If stored view is similar to input image, recognition would be simple and fast.

    How could this work?

    Images can be compared in parallel.

    Prev | Next

    VISIBILITY PROCESSING

    Rendering Polyhedra Scenes
    What is Visible?

    Prev | Next

    IMAGE BASED RENDERING

    Basic Idea

    Several pictures are taken from novel views in the environment. When rendering, these images are used to create views from new viewpoints. Very realistic rendering of environments without geometry.

    Issues

    What images should you combine in each region?
    At what point might you need to include a new image?
    Prev | Next

    COMPUTER VISION

    Using Aspect Graphs to Identify Convex Polyhedra

    Basic Idea

    Compute the VSP in 3-space for the object to be recognized. Since each region of the VSP has constant aspect, make a characteristic view for each region. Use these characteristic views to compare against the input image.

    Images can be compared in parallel.

    Observations

  • A face is always visible from viewpoints in front of it.
  • A face will become invisible only if viewer "goes below the horizon." DEMO?
  • There cannot be 2 vertices of the aspect graph for the same set of faces.
  • R^3 is subdivided by n planes for a polyhedron with n faces. The resulting subdivision is the VSP.

    • Complexity

  • Each plane intersects the other (n-1) planes forming O(n^2) vertices, edges and regions.
  • N planes form O(n^3) vertices and edges. Therefore there must be O(n^3) cells. VSP and aspect graph are also of order O(n^3).

    • Questions

    Constructing Aspect Graph

    Extend all faces of polyhedra. The resulting subdivision is the VSP. Place a node in each distinct region of VSP and connect nodes which share a common boundary.

    DEMO

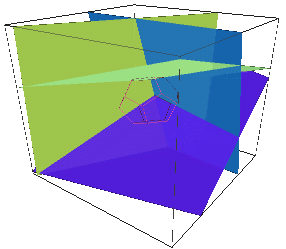
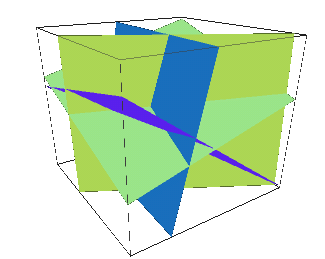
    Using Aspect Graph

  • Make characteristic views from each node of the aspect graph.
  • Given an input image, compare it to all stored characteristic views.
  • The input image should have same topological structure of one of the characteristic views if images came from the same 3D polyhedral object.

    • Example

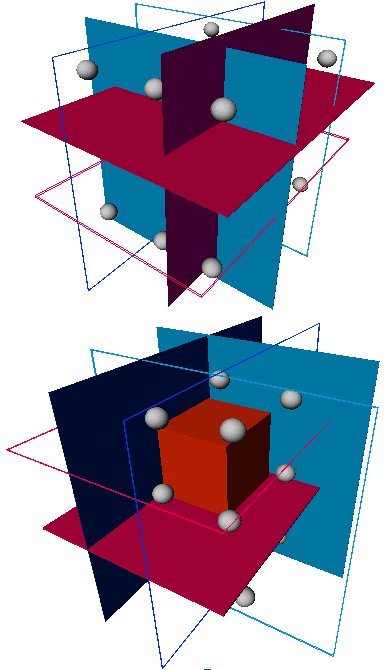    Prev | Next

    Using Aspect Graphs to Identify Non-Convex Polyhedra

    Observations

  • In the non-convex case, faces can occlude other faces.
  • Other types of events besides "horizon" event can occur. For example, edge-vertex (EV) and Edge-Edge-Edge (EEE).
  • EV Events: Plane Boundaries defined by a vertex and an edge involved in the visual event.
  • EEE Events: There is a surface of viewpoints from which three edges appear to intersect in a point.

    • Complexity

  • Surfaces in R^3 that bound regions of constant aspect involves triples of object edges.
  • There are O(n^3) triples of edges yielding O(n^3) such surfaces for a polyhedron of size n.
  • Since the surfaces are algebraic, any pair has a constant number of curves of intersection and any three have constant number of points of intersection. Thus the O(n^3) surfaces have O(n^9) intersection points.
  • VSP and Aspect graph O(n^9)!
    • Prev | Next

    TOPOLOGY CHANGE


    4-sided polygon


    5-sided polygon

    Prev | Next

    EVENT TYPES

    Edge Vertex: EV

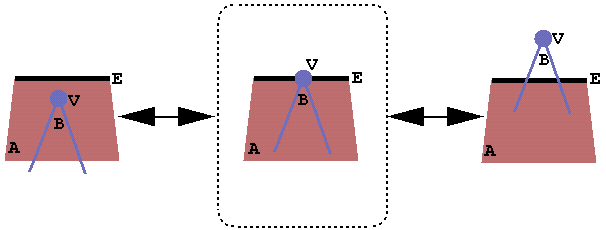
    DEMO

    Edge-Edge-Edge: EEE

    DEMO

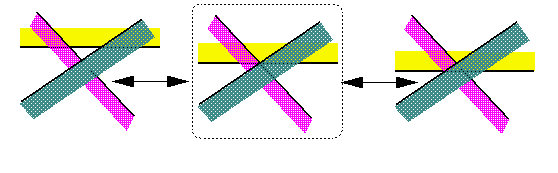
    Prev | Next

    COMPLEXITY

    Time And Space Complexity of VSP and Aspect Graph

    	Maximum size of the VSP
        -----------------------
                           Convex     Non-convex
			   Polyhedra  Polyhedra
        ------------------------------------------
        Orthographic       O(n^2)     O(n^6)
	Perspective	   O(n^3)     O(n^9)


	Construction time of the VSP & aspect graph
        -------------------------------------------
                           Convex     Non-convex
			   Polyhedra  Polyhedra
        --------------------------------------------
        Orthographic       O(n^2)     O(n^6 log n)
	Perspective	   O(n^3)     O(n^9 log n)

    Prev | Next

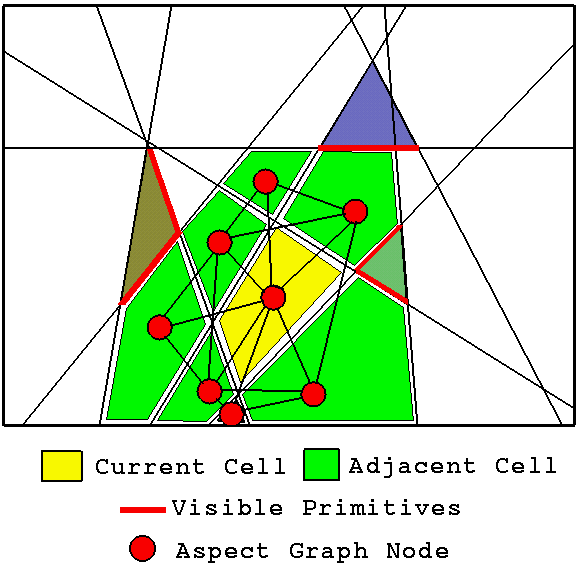
    Uses of VSP/Aspect Graph in Computer Graphics Visibility

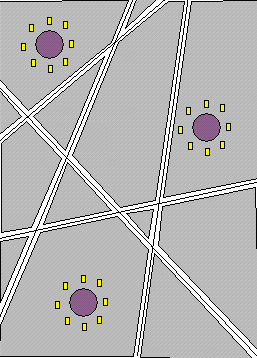
    Given a viewpoint and a polyhedral scene, an aspect graph could be used to deduce exact visibility. Below we have a 2D visualization of an aspect graph and viewpoint space partition. For each region the viewpoint is in, there is a corresponding node of the aspect graph. At each node of the aspect graph, information regarding what primitives are visible from each region is stored. Also, the links to other nodes (ie. regions) are stored.

    Prev | Next

    COMPRESSING ASPECT GRAPHS

    Linearized Aspect Graph

    A conservative approach to visibility which over-estimates the visible polygons in the scene from a viewpoint. The hardware z-buffer is used to resolve exact visibility for this superset of exact visibility. More crucially, the linearized aspect graph only catalogs VE (vertex-edge) events thus reducing the complexity of the aspect graph. Here's a naive algorithm for utilizing a linearized aspect graph for computing visibility:

    Precompuation:
	- Compute the aspect graph.  Catalog all VE events found

Runtime:
	--let A be the aspect graph containing B boundaries
	--let S be the set of visible polygons
	--let B be the set of polygons added 
	  or deleted by crossing boundary

	1. Find region containing viewpoint.
	2. S = {visible polygons from that region}
	3. while(!done)
		(wait for mouse input)
		forall B in A
			if (viewpoint crossed region boundary)
				S = S + B  (eg. S = S + p1 + p2 - p3 -p4)
		render S
	4. end

    Advantages:

    The algorithm only spends time reporting only visible changes, rather than recomputing visibility for each new viewpoint

    Disadvantages:

    Excessive time and storage of precomputation in creating the aspect graph. A scene of size n generates O(n^2) planes, partitioning the 3-dimensional space into O(n^6) cells. This implies that it needs atleast O(n^6) time to create the aspect graph. This makes it impractical for scenes containing more than a few tens of polygons.

    Prev | Next
    References

    [1] Satyan Coorg and Seth Teller. Temporally coherent conservative visibility. In Proc. 12th Annual ACM Symposium on Computation Geometry (1996).

    [2] Ziv Gigus and Jitendra Malik. Computing the Aspect Graph for Line Drawings of Polyhedral Objects. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 12, No. 2, February 1990.

    [3] Ziv Gigus and John Canny. Efficiently Computing and Representing Aspect Graphs of Polyhedral Objects. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 13, No. 6, June 1991.

    [4] Harry Plantinga and Charles Dyer. Visibility, Occlusion, and the Aspect Graph. Int. J. of Computer Vision, 5:2, 137-1609 (1990).

    +