Optimal Transport with Local and Global Structure
Generalizing the OT problem to include local structure (or ignore global invariances).
TL;DR: Vanilla OT is not always directly applicable, and if it is, it might not fully capture available structural information. We extend it to
- directly incorporate structural information
- be invariant to global linear transformations
- be invariant to global highly non-linear transformations
I. Injecting Structure into the OT Cost Objective
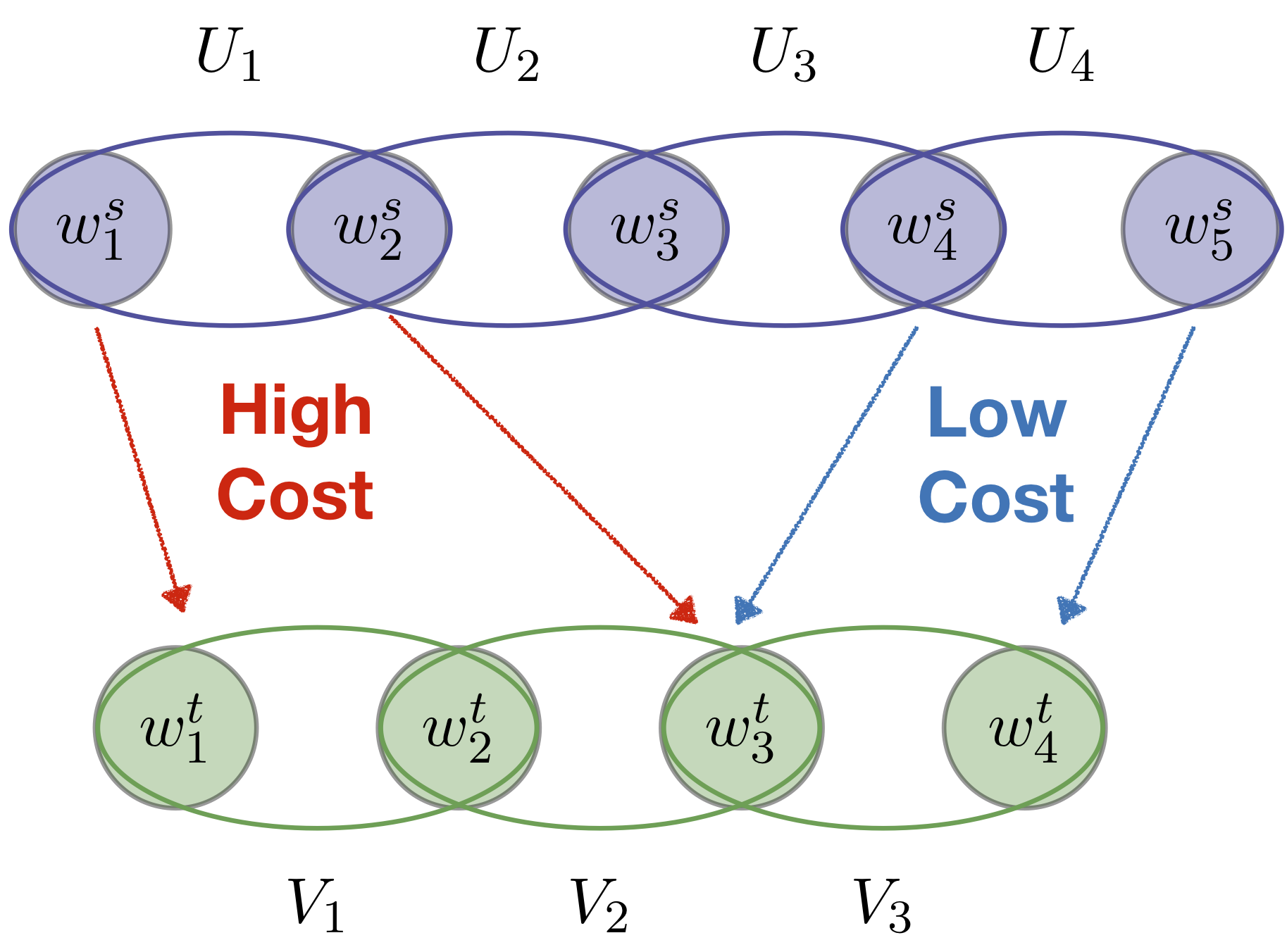
An important appeal of optimal transport distances is that they reflect the metric of the underlying space in the transport cost. Yet, in a number of settings, there is further important structure that remains uncaptured. This structure can be intrinsic if the distributions correspond to structured objects (e.g., images with segments, or sequences) or extrinsic if there is side information that induces structure (e.g., groupings). A concrete example arises when applying optimal transport to do- main adaptation, where a subset of the source points to be matched have known class labels. In this case, we may desire source points with the same label to be matched coherently to the same compact region of the target space, preserving compact classes, and not be split into disjoint, distant locations (Courty et al., 2017). When pairing control and treatment units in observational studies of treatment effects, it is beneficial to compare treated and control subjects from the same “natural block” (e.g., family, hospital) so as to minimize the difference between unmeasured covariates (Pimentel et al., 2015). In all these examples, the additional structure essentially seeks correlations in the mappings of “similar” source points. Such dependencies, however, cannot be induced by standard formulations of optimal transport whose cost is separable in the mapping variables; they require nonlinear interactions.
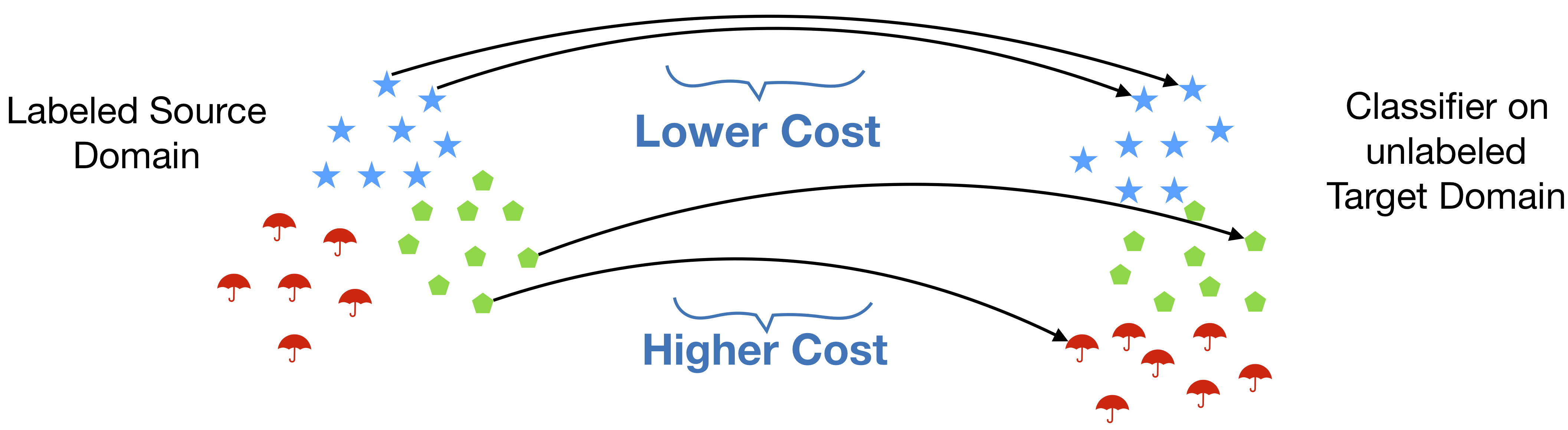
In this work, we develop a framework to incorporate such structural information directly into the OT problem. This novel formulation opens avenues to a much richer class of (nonlinear) cost functions, allowing us to encode known or desired interactions of mappings, such as grouping constraints, correlations, and explicitly modeling topological information that is present, for instance, in sequences and graphs. The tractability of this nonlinear formulation arises from polytopes induced by submodular set functions. Submodular functions possess two highly desirable properties for our problem: (1) they naturally encode combinatorial structure, via diminishing returns and as combinatorial rank functions; and (2) their geometry leads to efficient algorithms.
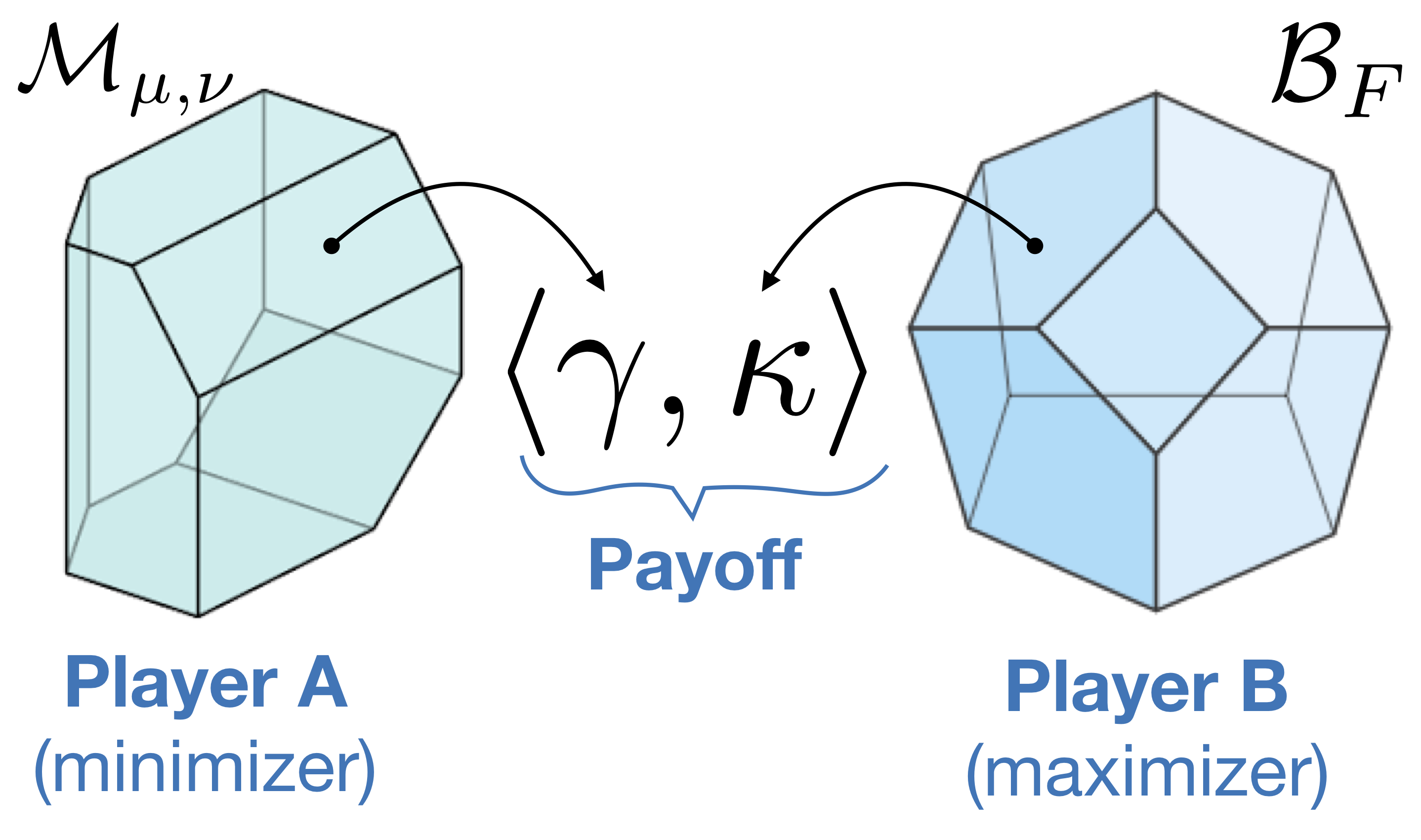
The resulting combination of the geometries of transportation and submodularity leads to a problem with rich, favorable polyhedral structure and connections to game theory and saddle point optimization. We leverage this structure to solve the submodular optimal transport problem via a saddle-point mirror-prox algorithm involving alternating projections onto the polytope defined by the transportation constraints and the base polytope associated with the submodular cost function.
Via various applications and experiments, we show how different submodular functions yield solutions that interpolate between strictly structure-aware transportation plans and structure-agnostic regularized versions of the problem. Besides these synthetic experiments, we evaluate our framework in two real-life applications: domain adaption for digit classification and sentence similarity prediction. In both cases, introducing structure leads to better empirical results.
II. Making OT invariant to global transformations
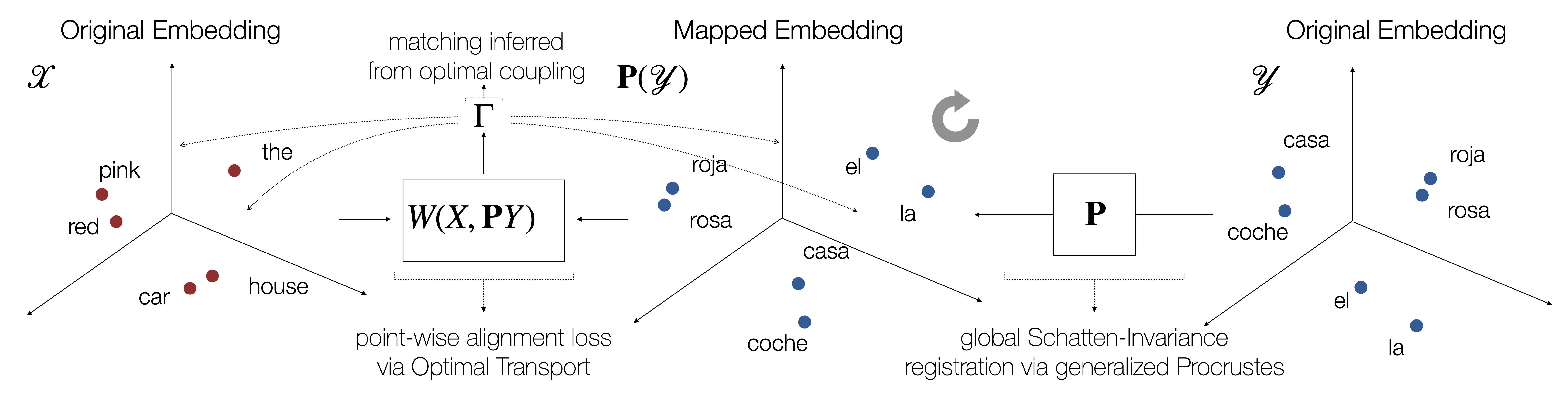
A key limitation of classic OT is that it implicitly assumes that the two sets of objects in question are represented in the same space, or at least that meaningful pairwise distances between them can be computed. This is not always the case, especially when the objects are represented by learned feature vectors. For example, word embedding algorithms operate at the level of inner products or distances between word vectors, so the representations they produce can be arbitrarily rotated, sometimes even for different runs of the same algorithm on the same data. Such global degrees of freedom in the vector representations render direct pairwise distances between objects across the sets meaningless. Indeed, OT is locally greedy as it focuses on minimizing individual movement of mass, oblivious to global transformations.
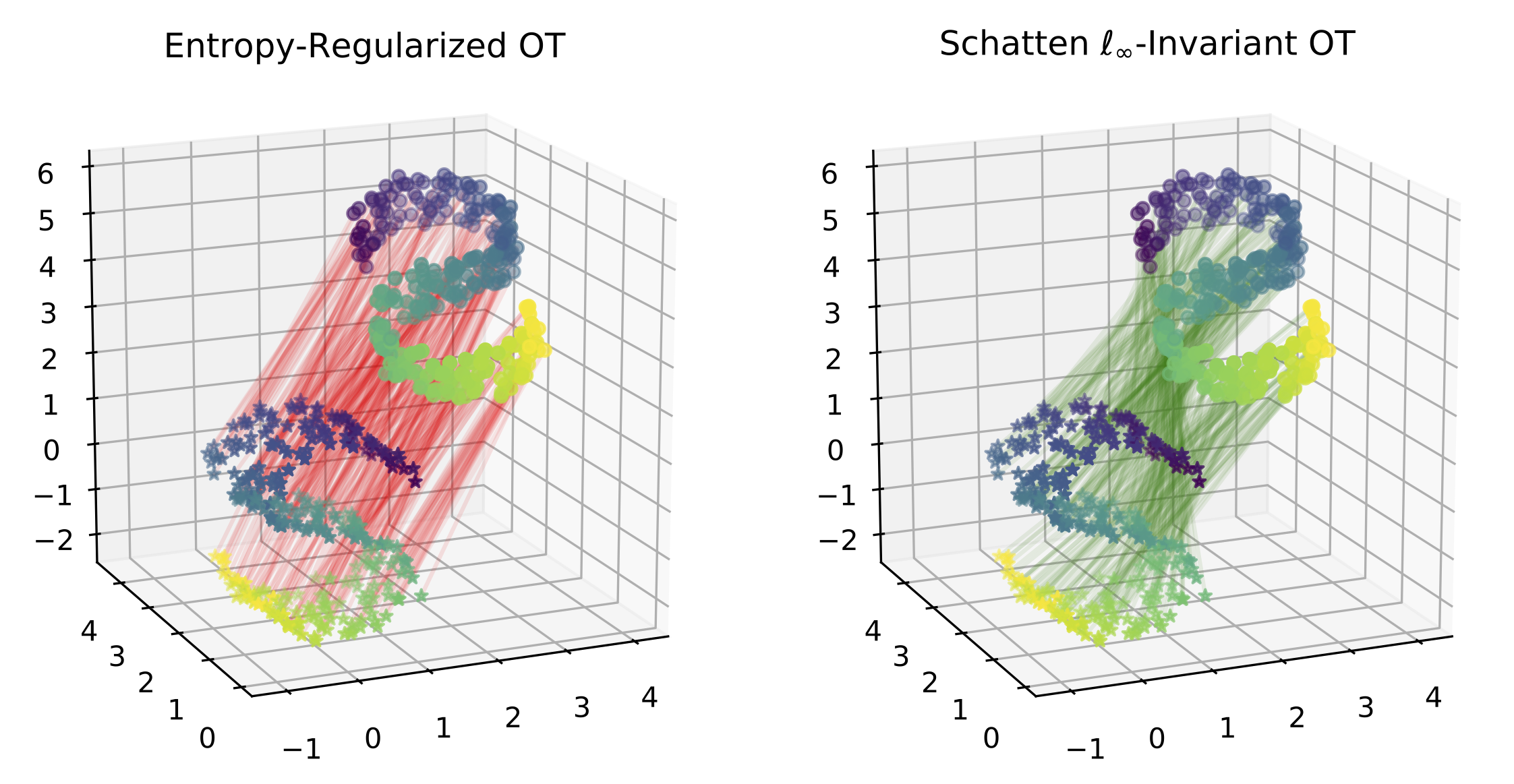
In this work, we propose a general framework for optimal transport in the presence of latent global transformations. We cast the problem as a joint optimization over transport couplings and transformations chosen from a flexible class of invariances (defined as Schatten $\ell_p$-norm balls), propose algorithms to solve it, and show promising results in various tasks, including a popular unsupervised word translation benchmark.
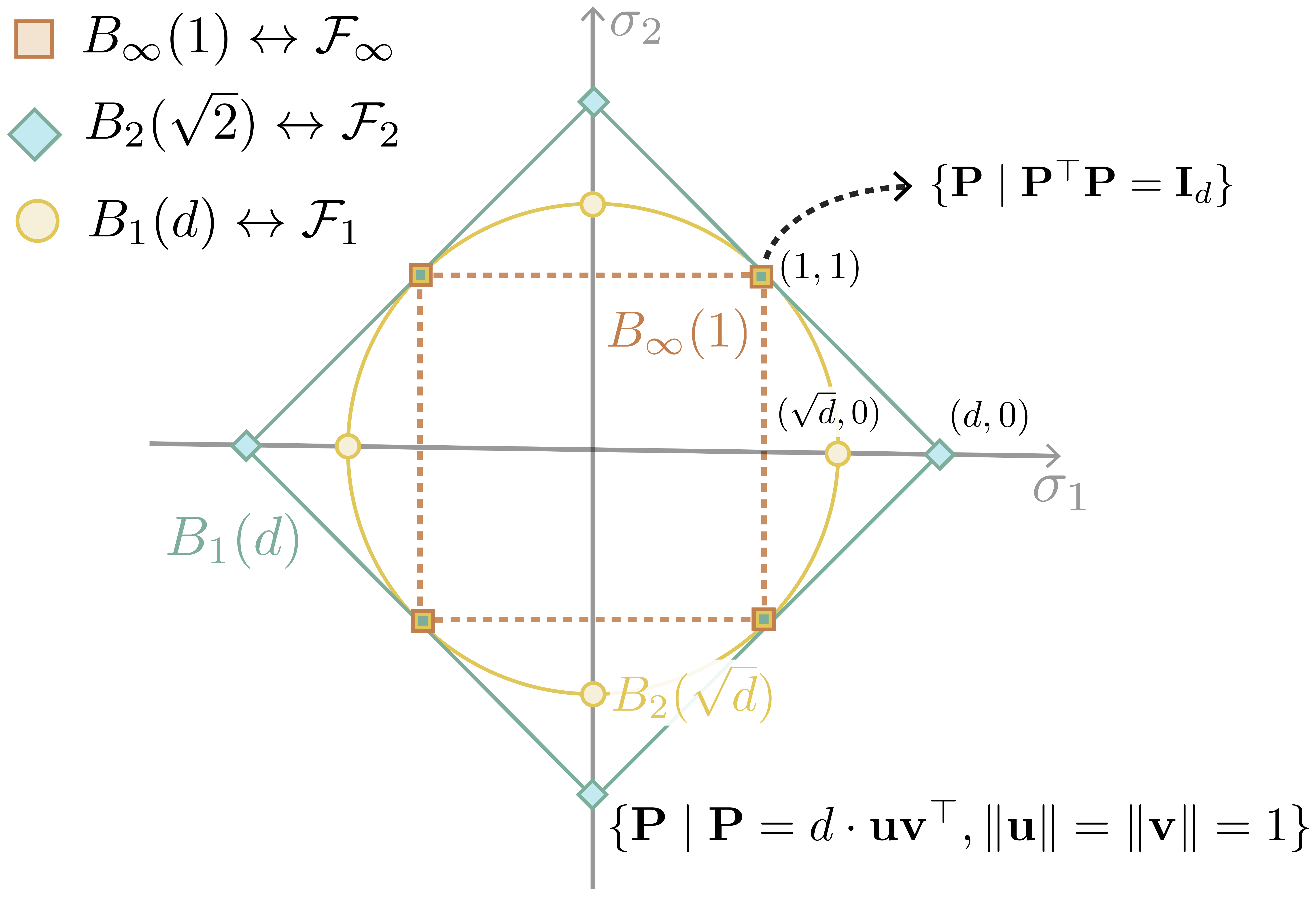
Our framework is very general and allows various types of invariances to be encoded. Moreover, our approach unifies previous methods for fusing OT with global transformations such as Procrustes mappings (Rangarajan et al., 1997; Zhang et al., 2017b; Grave et al., 2018), and reveals unexpected connections to the Gromov-Wasserstein distance (Mémoli, 2011).
III. OT on Hyperbolic Spaces
Hierarchical structures are ubiquitous in various domains, such as natural language processing and bioinformatics. For example, structured lexical databases like WordNet are widely used in computational linguistics as an additional resource in various downstream tasks. On the other hand, ontologies are often used to store and organize relational data. Building such datasets is expensive and requires expert knowledge, so there is great interest in methods to merge, extend and extrapolate across these structures. A fundamental ingredient in all of these tasks is matching1 different datasets, i.e., finding correspondences between their entities. For example, the problem of ontology alignment is an active area of research, with important implications for integrating heterogeneous resources, across domains or languages. On the other hand, there is a long line of work focusing on automatic WordNet construction that seeks to leverage existing large WordNets (usually, English) to automatically build WordNets in other low-resource languages.
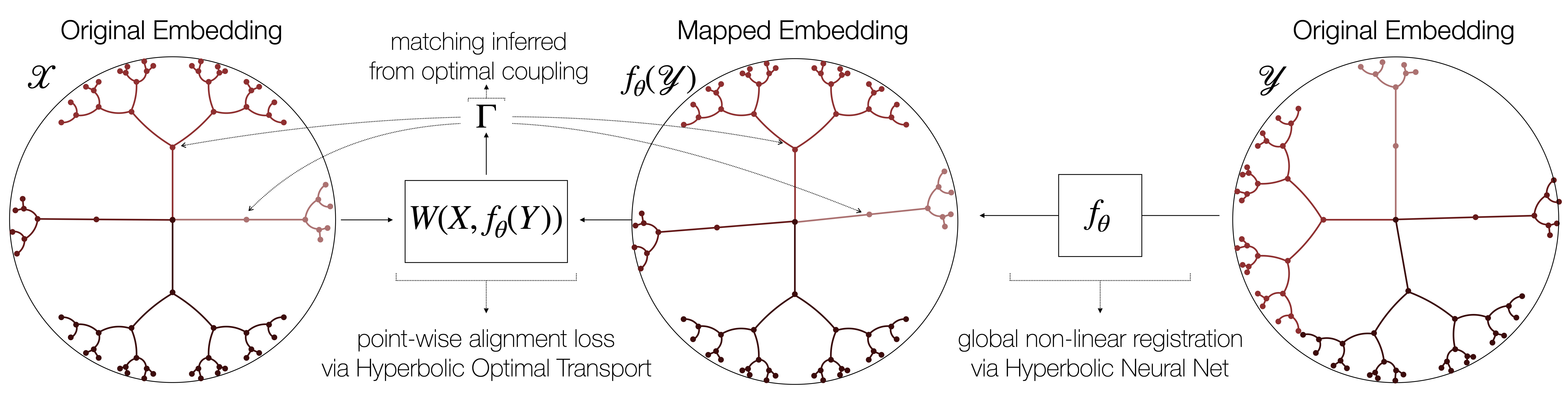
Our work builds upon two recent trends in machine learning to derive a new approach to this problem. On one hand, there is mounting evidence —both theoretical and empirical— of the advantage of embedding hierarchical structures in hyperbolic (rather than Euclidean) spaces. On the other hand, various fully unsupervised geometric approaches have recently shown remarkable success in unsupervised word translation. We seek to combine these two recent developments by extending the latter to non-Euclidean settings, and using them to find correspondences between datasets by relying solely on their geometric structure, as captured by their hyperbolic-embedded representations. The end goal is a fully unsupervised approach to the problem of hierarchy matching.
In our work, we focus on the second step of this pipeline —the matching— and assume the embeddings of the hierarchies are already learned and fixed. Our approach proceeds by simultaneous registration of the two manifolds and point-wise entity alignment using optimal transport distances. After introducing the building blocks of our approach, we begin our analysis with a set of negative results. We show that state-of-the-art methods for unsupervised (Euclidean) embedding alignment perform very poorly when used on hyperbolic embeddings, even after modifying them to account for this geometry. The cause of this failure lies in a type of invariance —not exhibited by Euclidean embeddings— which we refer to as branch permutability. At a high level, this phenomenon is characterized by a lack of consistent ordering of branches in the representations of a dataset across different runs of the embedding algorithm, and is akin to the node order invariance in trees.
Relevant Publications:
- Alvarez-Melis, Jaakkola and Jegelka. “Structured Optimal Transport”, AISTATS 2018.
- Alvarez-Melis, Jegelka and Jaakkola. “Towards Optimal Transport with Global Invariances”, AISTATS 2019.
- Alvarez-Melis, Mroueh and Jaakkola. “Hierarchy Matching with Optimal Transport over Hyperbolic Spaces”, OTML@NeurIPS2019.
