|
Noga Alon, |
|
Algorithmic Construction of Sets for k-Restrictions, |
In the problem of Set-Cover, one is given n points and m
subsets whose union contains all n points. The goal is to cover all points
using as few subsets as possible.
|
|
Prior to our work [Alon-Moshkovitz-Safra], it was known that the problem Set-Cover can be approximated to within lnn by a polynomial-time algorithm [Lovász75]. On the negative side, two results were known:
1. (Strong assumption, Tight conclusion) If NP * DTIME(nO(loglogn)), then Set-Cover cannot be approximated to within (1-e)×lnn by a polynomial time algorithm, for any e>0 [Feige95].
2. (Traditional assumption, Non-tight conclusion) If P¹NP (i.e., NP * DTIME(nO(1))), then Set-Cover cannot be approximated to within c×lnn by a polynomial time algorithm, for some constant 0<c<1 [Raz-Safra97, Arora-Sudan97].
The second result follows from a sub-constant error PCP constructed by [Raz-Safra97, Arora-Sudan97]. The motivation for the paper [Alon-Moshkovitz-Safra] was to obtain tighter inapproximability results for Set-Cover, given the sub-constant error PCP of [Raz-Safra97, Arora-Sudan97].
Indeed, we found an adaptation of the classic Set-Cover reductions that allowed us to tighten the inapproximability result. Let us be more specific. Going into the Set-Cover reduction reveals that the constant c in the statement of the second result is c=1/(2ln2×(d+1)), where d is the number of queries in the PCP. We manage to reduce c to (essentially) c»1/(lnd+1), namely to reduce the dependency in d to logarithmic (while the "truth" seems to be that there is no dependence in d at all). The number of queries d is some constant that was not optimized by [Raz-Safra97, Arora-Sudan97] or by later work [Dinur-Fischer-Kindler-Raz-Safra99], however, our results improve the previous results no matter what the d actually obtained is.
To derive our improvement, we extended the beautiful framework of [Naor-Schulman-Srinivasan95] that provides algorithmic constructions of sets for k-restriction problems (more details about these follow). Interestingly, for our extension we needed a theorem from algebraic topology called The Necklace Splitting Theorem [Alon87].
At the same time, we generalized
the framework of [Naor-Schulman-Srinivasan95] to provide efficient
constructions for other problems, such as group testing and generalized
hashing. As building blocks for the constructions we used multi-way
splitters. Multi-way splitters are refinements of objects, called splitters, that lie in the heart of the
[Naor-Schulman-Srinivasan95] framework. Multi-way splitters seem to be
interesting in their own right, and it is their construction that requires the
Necklace Splitting Theorem. More details can be found in the paper.
k-Restriction ProblemsTo explain what k-restriction problems are, let us use the following metaphor (that appeared in an earlier version of the paper): A Goldsmith makes some sort of objects, say strings in {0,1}n. Someone who is very hot-tempered [the Pirate] comes and asks the Goldsmith to create an object. But, this someone is also very capricious, so when he comes to collect the object, he can come up with some local demand on the string he didn’t make in advance (among a large set of demands). For example, the Pirate may point to some k places in the string and say that he wanted an even number of 0’s and 1’s in these positions. This hot-tempered Pirate would decapitate the Goldsmith if the string does not match his demand. Formally, we model a demand by a Boolean function f:{0,1}k®{accept, reject}. The Pirate has a set of possible demands f1,…,fs (known to the Goldsmith) and he may point to any k positions 1 £ i1<…<ik £ n, and decide on any demand 1 £ j £ s. The Goldsmith’s string xÎ{0,1}n must satisfy fj(xi1…xik) = accept. The idea is that the Goldsmith would prepare many strings, and not just one, so, no matter what the demand is, the Goldsmith has a way to meet it. The Goldsmith would like to make as few strings as possible. It turns out that this metaphor captures many combinatorial problems that arise in Computer Science. All of them can be solved using any (almost) k-wise independent distribution. However, we wish to obtain considerably smaller solutions. The key point is that here the constraints are merely existential, namely we wish to argue that there exists a string, rather than argue something for many of the strings. |
|
|
|
Our Results
A common approach to k-restriction problems uses the probabilistic method.
Assume that D is a distribution over strings in {0,1}n, and that for any k positions 1 £ i1<…<ik
£ n and
any demand 1 £ j £ s, the probability that a string x, drawn
from the distribution D, satisfies the demand fj
at these positions, is at least e. A calculation shows that in this case,
there necessarily exists a solution for the k-restriction problem of size (klnn+s)/e (up to rounding).
The question is: can we find a solution that is as good, using an efficient deterministic algorithm?
Let us assume that D is a
product distribution that is given as input. The uniform distribution,
addressed by [Naor-Schulman-Srinivasan95] is an example. Yet many times other
product distributions are more appropriate. This is the case with group
testing. In the group testing problem, among n people, at most (k-1) carry
a fatal virus. We wish to detect the carriers exactly. Now, there is a
test that detects the virus in blood samples, but the test is very expensive.
Thus, we wish to perform as few tests as possible. The idea is to test groups,
i.e., run tests on many blood samples mixed together. This way, if a test comes
out negative, we know that none of its blood samples had the virus, while if
the test comes out positive, other tests should single
out the carrier(s). It can be checked that the best distribution for this
problem decides on a mix by picking each individual independently with
probability 1/k.
We have several results for k-restriction problems, suitable for different ranges of the parameter k.
1. For k=O(1), there is an algorithm running in time polynomial in s and nk that outputs a solution of size arbitrarily close to the probabilistic size. The algorithm uses the method of conditional expectations on an approximation of D (It is known that any product distribution is k-wise efficiently approximable, by a result of Even et al [EGLNV98]).
2. For k=O(logn/loglogn), we use an idea of [Naor-Schulman-Srinivasan95] to compose an inefficient algorithm for a k-restriction problem with a construction of a perfect hash family, to obtain an efficient algorithm producing slightly larger solutions.
3. For k=O(logn), we do not have a general theorem, but rather a
Divide-and-Conquer framework for generating efficient algorithms. This
framework is a generalization via the Necklace Splitting Theorem of the
[Naor-Schulman-Srinivasan95] framework. We demonstrate it by obtaining
algorithms for generalized hashing and for finding a Set-Cover gadget.
The overhead introduced by this framework is considerably larger than that
introduced in 1 and 2, but for the Set-Cover reduction, for example, it is
affordable.
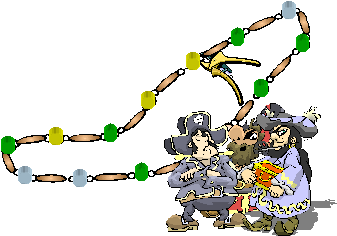
The Necklace Splitting TheoremWe conclude with a brief overview of The Necklace Splitting Theorem. The Theorem got its name from the following metaphor: Suppose that b thieves steal a necklace with beads of t types. They want to cut it in as few places as possible and fairly divide it between them. You can assume that the number of thieves b divides the number of beads of each type, so a division in which each thief gets the same number of beads of each type is possible. In the paper we actually generalized the theorem to an arbitrary number of beads of each type. In this case, we want the division to be "fair up to rounding". The generalization was obtained using network flows. It is easy to observe that if the necklace contains first the beads of the first type, then the beads of the second type, etc., then (b-1)t cuts are needed. The Necklace Splitting Theorem shows that this is the worst possible, namely, (b-1)t cuts always suffice. |
|
|
|
|
||
|