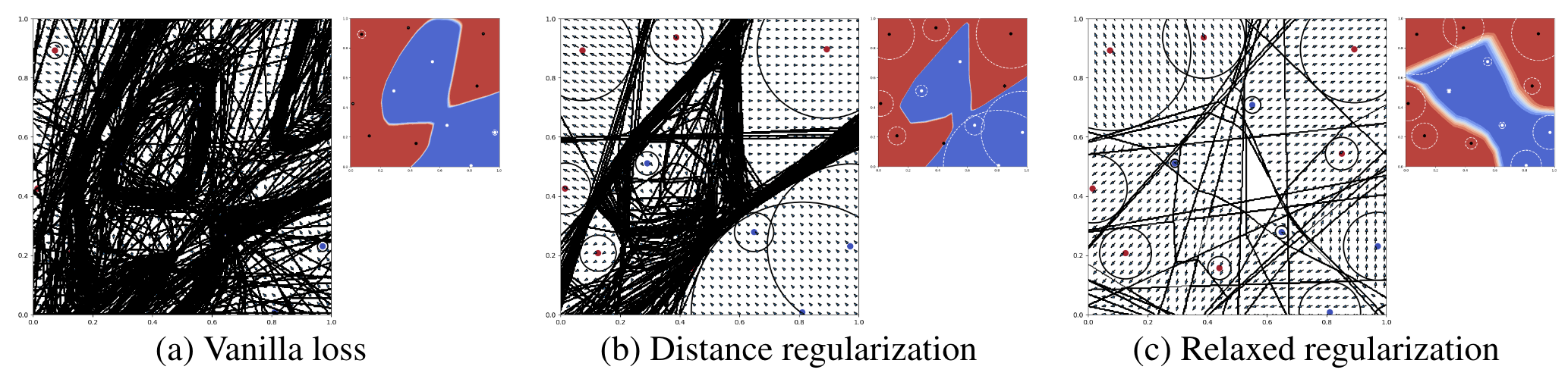
Figure 1: Toy examples of a synthetic 2D classification task. For each model (regularization type), we show a prediction heatmap (smaller pane) and the corresponding locally linear regions. The boundary of each linear region is plotted with line segments, and each circle shows the L2 margin around the training point. The gradient is annotated as arrows with length proportional to its L2 norm.
Abstract
Deep networks realize complex mappings that are often understood by their locally linear behavior at or around points of interest. For example, we use the derivative of the mapping with respect to its inputs for sensitivity analysis, or to explain (obtain coordinate relevance for) a prediction. One key challenge is that such derivatives are themselves inherently unstable. In this paper, we propose a new learning problem to encourage deep networks to have stable derivatives over larger regions. While the problem is challenging in general, we focus on networks with piecewise linear activation functions. Our algorithm consists of an inference step that identifies a region around a point where linear approximation is provably stable, and an optimization step to expand such regions. We propose a novel relaxation to scale the algorithm to realistic models. We illustrate our method with residual and recurrent networks on image and sequence datasets.
- Keywords: robust derivatives, transparency, interpretability.
- TL;DR: a scalable algorithm to establish robust derivatives of deep networks w.r.t. the inputs.
- Code: GitHub repo