
Futility pruning at frontier nodes saves a lot of work by deciding in advance which moves will cause a ``stand pat'' beta cutoff at the direct successor nodes on the search horizon. This requires the search to determine lower bounds for the static evaluation scores of horizon nodes based on the situations and moves at frontier nodes. Such bounds are easy to obtain for non-checking moves and typical chess evaluation functions that simply add material balances and positional scores.

With max posn score denoting a constant upper bound on the absolute values of all positional scores, the term mat balance(node) - max posn score represents a tight lower bound for the static score of a node as computed by typical evaluation functions. This tight lower bound allows for the formulation of a theoretically sound futility condition at frontier nodes that enables the advance detection of subsequent ``stand pat'' beta cutoffs for non-checking moves. The theoretical soundness of the futility condition follows from the well-known relations of alpha, beta, and the material balances at direct successors of a node.
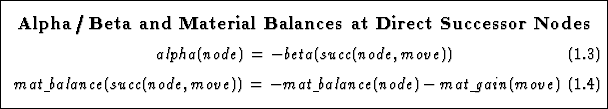

Given a suitable value for max posn score, it is therefore safe to simply cut off all non-checking moves at frontier nodes for which the futility condition mat balance(node) + mat gain(move) + max posn score <= alpha(node) holds. The according futility cutoff-rate heavily depends on the value of max posn score and the material balances of the positions encountered during the search. The tighter the bound on positional scores (i.e., the smaller max posn score) and the greater the material imbalances are, the more cutoffs occur.