How Quackle Plays Scrabble

By Jason Katz-Brown and John O'Laughlin

This document aims to explain Quackle's artificial intelligence (AI) and the algorithms it uses.

Quackle's AI in a Block Diagram

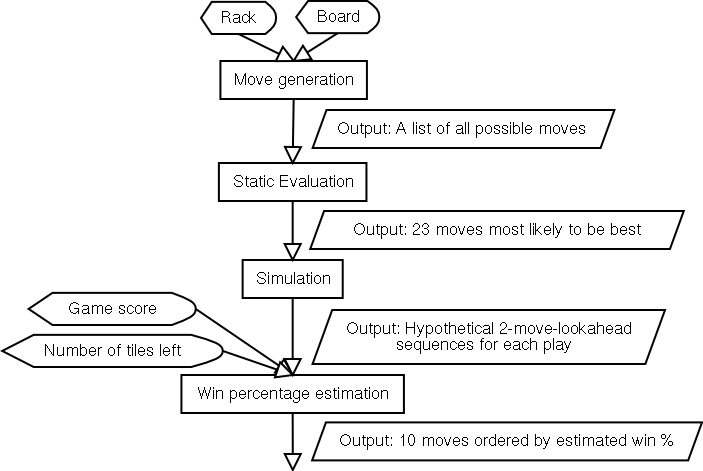
The conniveries of each block are explained below.

Move Generation

This block takes a rack and board as input and very quickly outputs a list of all possible plays that can be made. Quackle's ultrafast move generator uses the Scrabble lexicon converted into a GADDAG. The GADDAG data structure was originally designed by Steven A Gordon, and uses the move generation algorithm he outlined in A Faster Scrabble Move Generation Algorithm).

Static Evaluation

This block takes a list of moves as input and very quickly outputs a list of moves ordered by a rough guess at how strong they are. For each play, this "static evaluation", so called because there is no look-ahead involved, is simply the score of the play plus an estimated "leave value" of the letters left on the player's rack after making the play. For instance, if the rack is ACEENOR, and Quackle wants to statically evaluate a play of OCEAN where it scores 19 on the board, the result is 19 plus the value of the leave ER. This leave value is gleaned from a table lookup into a large precomputed database of all possible one to six letter leaves. Here is a typical sequence of entries:

Leave	Value
`EQYZ`	-4.68
`EQZ`	-4.12
`ER`	4.79
`ERR`	0.39
`ERRR`	-9.02

So the final static evaluation of the OCEAN play is 19 + 4.79 = 23.79. The static evaluation is computed for all other plays and the 23 plays with highest static evaluation comprise the output list. The database of leave values distributes high values to leaves with good chance of allowing "bingos", or plays that use all 7 letters and score a 50-point bonus, in coming turns. The database also favors leaves that garnered high scores when they appeared on a player's rack in a large sample of Quackle versus Quackle games.

Simulation

This block takes a list of moves as input (let's call this the candidate list) and slowly outputs, for each candidate play, hypothetical future positions that are reached after the following sequence of events:

The current player puts the candidate play (let's call it ply_0) on the board;
The opponent draws 7 random tiles, performs a static analysis of this new position after ply_0, and puts the play (ply_1) with the highest static evaluation on the board;
The current player replenishes his rack with random tiles, performs a static analysis of this new position after ply_0 and ply_1, and puts the play with the highest static evaluation (ply_2) on the board.
The current player adds to his score the value of his rack leave after ply_2.

The end result of this process is that the current player's score is equal to his score in the original position plus the scores of ply_0 (the candidate), ply_2, and the value of his leave after making ply_2. The opponent's score is equal to his score in the original position plus the score of ply_1. Let's look at an example. Let's assume that the current player is ahead by 20 points and holds ACEENOR. Now let's say we're looking at the candidate OCEAN and iteration 1 goes:

Current player plays OCEAN for 19 points leaving ER
Opponent randomly draws AIIKNST and plays TANKINIS for 167.
Current player randomly draws PQXYZ to his ER so holds EPQRXYZ. He plays PR(O)XY for 50 leaving EQZ.

After this sequence, the current player is down by 86 points (20 + 19 - 167 + 50 = -78). The value of his EQZ leave is -4.12, so the final outcome of this iteration for OCEAN is a point differential of -82.12. This process is repeated many times to get many hypothetical positions for each candidate play. Quackle performs about 300 iterations of this process for each candidate move. Simulation is similar to the look-ahead algorithms used in chess artificial intelligence, but modified to handle the randomness inherent in the outcome of a Scrabble game. Instead of performing one look-ahead very many moves ahead, we perform many looks ahead of only 2 moves into the future.

Win Percentage Estimation

This block takes many future positions for each candidate and very quickly outputs a list of plays ordered by estimated win percentage. For each future position, Quackle does a simple table lookup into a precomputed database that guesses the current player's chance of winning the game based on how many points he is ahead or behind and how many tiles are left to be played in the game (the sum of the 7 tiles on the opponent's rack and the number of tiles left in the bag). For each candidate, these win percentage estimates are averaged over all the future positions that started out with that candidate.

Here is a sample of the win percentage estimation database:

Point differential	Number of tiles left	Estimated win probability
-82	65	0.203748
-82	66	0.20625
-82	67	0.208717
...
9	15	0.784516
9	16	0.779248
9	17	0.774146

Let's say we're trying to guess the win percentage of the OCEAN play from before after our first iteration of simulation. Recall the point differential after iteration 1 was -82.12. Let's assume that after the last play of that iteration, PROXY, there were 66 tiles remaining in the game. Then we'll estimate that if the resulting game from OCEAN's iteration 1 were played to completion, the current player would win about 20.6% of the time.

The database of estimated win probabilities was made by analyzing the distribution of wins over many Quackle versus Quackle games.

This kind of win-percentage-based analysis is critical in a Scrabble AI when needing to erase a large deficit or protect a lead. For instance, when down by 70 points late in the game, a bingo is usually necessary to catch up. If the current player ever bingos in an iteration of a candidate's simulation the estimated win percentage of that candidate is boosted mightily, while most other iterations will have an estimated win percentage of about zero. After averaging the estimated win percentages of all iterations for a candidate, the plays that have the greatest chance of a future bingo, will come out on top as desired.