Many real-world data such as text and XML documents exhibit a rich internal structure.
Consider for instance natural language sentences and XML document.
Parsing based on grammars allows us to find tree structures representing the internal
organization of these data. Consider the following grammar (syntax exmplained below)
Example
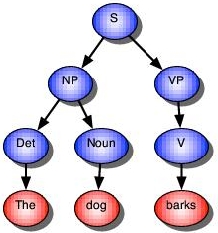
S -> NP, VP. VP -> V. NP -> Det, Noun. Det -> the. Noun -> dog. V -> barks. |
Using this grammar, the sentence The dog barks can be parsed yielding the tree

These trees are useful for a wide variety of tasks, including semantic interpretation, information retrieval, and machine translation. Unfortunately, most data have a large number of possible structures and are typically noisy. Naive Bayes, hidden Markov models, and Bayesian networks cannot - at least elegantly - represent the internal tree structure. Probabilistic grammars provide tools to address the resulting ambiguities. Here, we will focus on probabilistic context free grammars.
A probabilistic context free grammar (or PCFG) is a context free grammar that associates a probability with each of its productions. It generates the same set of parses for a text that the corresponding context free grammar does, and assigns a probability to each parse. The probability of a parse generated by a PCFG is simply the product of the probabilities of the productions used to generate it.
More formally, let T be a terminal alphabet and N a nonterminal alphabet.
A probabilistic context-free grammar (PCFG) G consists of a distinguished start symbol
S in N plus a finite set of productions of the form
| p : X -> alpha, |
where X is in N,alpha is
in the power set of N u T, and p is a probability value.
The probability values for all production rules of X sum up to 1.0.
A PCFG defines a stochastic process with sentential forms as states, and leftmost rewriting steps as transitions. We denote a single rewriting operation of the grammar by a single arrow ->. If as a result of one ore more rewriting operations we are able to rewrite and element beta of the powerset of N u T as a sequence gamma of nonterminals and terminals, then we write beta ->* gamma.The probability of this rewriting is the product of all probability values associated to productions used in the derivation.
As for HMMs, there are three main problems associated with PCFGs: