We want computers to be able to localize sounds better. Human listeners can successfully localize sounds even in noisy and reverberant environments. Computer systems can localize sounds well in quiet, anechoic environments, but their performance is poor in reverberant environments. One reason for this performance gap is that human listeners exhibit the precedence effect, in which they weigh localization cues from sound onsets more heavily when making localization judgements. This effect has been well-studied in the psychoacoustics literature but has not yet been integrated into a practical computer system for audio localization.
Audio source localization is important for people's normal environmental awareness and interpersonal interactions. Without it, for example, it would be more difficult to locate a ringing cellular phone or a friend who calls your name in a crowded room. To enable computers to perform well in such typical human scenarios, accurate sound localization is essential. In addition, better localization can improve subsequent speech enhancement or speech recognition.
The precedence effect is a psychoacoustic effect in which the apparent location of a sound is influenced most strongly by the localization cues from the initial onset of the sound [1, 2]. For example, when human listeners report the location of a rapid sequence of clicks, they tend to report the location of the initial click even if later clicks in the sequence came from other directions [3]. Because direct path sound arrives before any reflections, initial onsets will tend to be less corrupted by reverberation than subsequent sounds, and the precedence effect improves people's ability to localize sounds in reverberant environments.
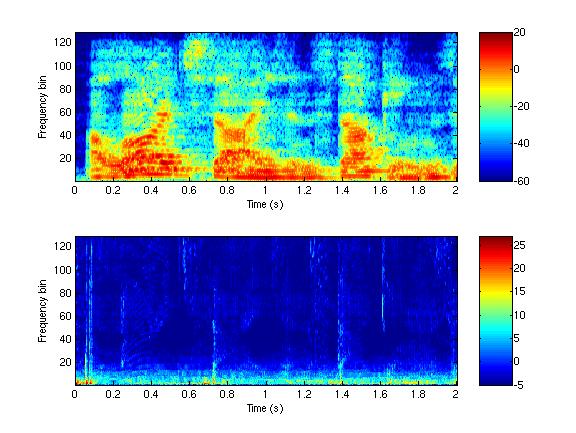
Figure 1 shows a spectrogram of reverberated speech and the associated time-frequency map of localization precision. Sudden onsets in the spectrogram correspond to time-frequency regions with more reliable localization information. This example was generated by simulating reverberation in a room and averaging the squared localization error across many possible configurations of sound source and microphones.
We take inspiration from the precedence effect and learn a function that takes a reverberant speech spectrogram as input and produces a time-frequency map of localization precision as output. Currently, this mapping takes the form of a finite impulse response (FIR) filter.
 |
| Figure 1: Empirical justification for the precedence effect. Top is a spectrogram of reverberated speech. Bottom is a time-frequency plot of the empirical localization precision (in dB). Sudden onsets in the spectrogram, such as those at 0.07, 0.7, and 1.4 seconds, correspond to time-frequency regions with high localization precision. |
We use our localization precision maps in the generalized cross-correlation (GCC) framework [4] to localize sounds. As described in [5] and [6], our results are better than the results for the phase transform, a standard GCC technique for use in reverberant environments.
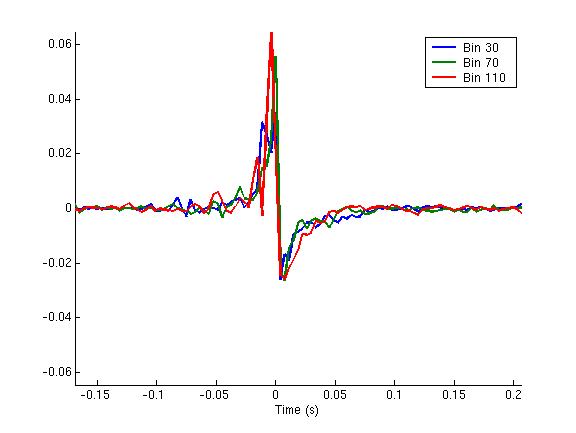
In addition to the demonstrated performance improvements, our learned mappings are consistent with the precedence effect. Three of our FIR filter mappings are shown in Figure 2, along with a schematic decomposition. Our learned filters are sensitive to onsets even though we did not explicitly constrain them to be onset detectors.
 |
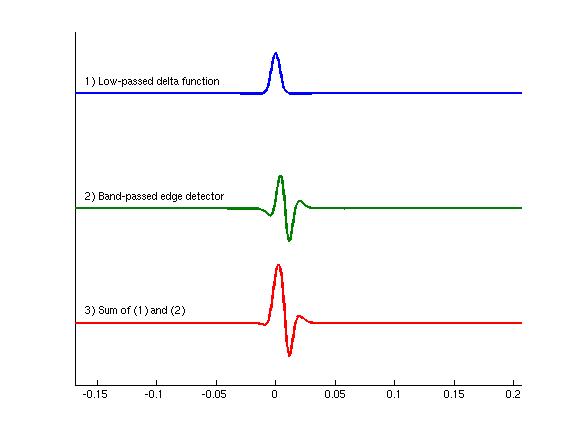 |
| Figure 2: Narrowband filters. Left is a representative subset of the learned narrowband filters. Right is a schematic decomposition of the filters. Each of the learned narrowband filters can be viewed as a linear combination of a low-pass filtered impulse (top) with a band-pass filtered edge detector (middle). The bottom curve shows the linear combination of the top two curves, which is qualitatively similar to the learned filters. | |
Our system works well for speakers in stationary background noise, but nonstationary background noise degrades performance. By using training data with nonstationary noise, including competing speakers, in combination with more sophisticated regression techniques, we are in the process of addressing this issue. These enhancements will allow for a richer description that simultaneously captures the structure of typical room acoustics and the structure of human speech.
In addition, because we estimate the uncertainty of localization cues in individual time-frequency regions, we should be better able to use these cues to compute time-frequency masks for source separation in reverberant environments.
This research was carried out in the Vision Interface Group, and was supported in part by DARPA and Project Oxygen.
[1] R. Y. Litovsky, H. S. Colburn, W. A. Yost, and S. J. Guzman. The precedence effect. In The Journal of the Acoustical Society of America, vol. 106, no. 4, pp. 1633-1654, 1999.
[2] P. M. Zurek. Directional hearing. W. A. Yost and G. Gourevitch, Eds. Springer-Verlag, 1987. chapter "The precedence effect".
[3] G. C. Stecker. Observer weighting in sound localization. Ph.D. dissertation, University of California at Berkeley, 2000.
[4] C. H. Knapp and G. C. Carter. The generalized correlation method for estimation of time delay. In Transactions on Acoustics, Speech, and Signal Processing. vol. 24, no. 4, pp. 320-327, 1976.
[5] K. Wilson and T. Darrell. Improving audio source localization by learning the precedence effect. In The Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, 2005
[6] K. Wilson and T. Darrell. Learning the precedence effect in the generalized cross-correlation framework. IEEE Transactions on Speech and Audio Processing, 2006 (to appear).