MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001--Structure and Interpretation of Computer Programs
Fall Semester, 1997
Problem Set 2
Issued: September 16, 1997
Due: In Recitation, Wednesday September 24
Tutorial exercises due: in tutorial, the week of September 22
Reading: Complete Chapter 1 of SICP.
Do exercise 1.16 of the text.
Do exercise 1.17 of the text.
Do exercise 1.26 of the text.
Procedure repeated takes as arguments a procedure p and a number n, where p itself takes one argument, and returns a new procedure of one argument by ``composing p with itself n times.'' Namely,
(define (repeated p n)
(if (zero? n)
(lambda (x) x)
(lambda (x) (p ((repeated p (dec n)) x)))))
Determine the values of the expressions
((repeated square 2) 5)
and
((repeated square 5) 2).
In tutorial you may be asked how the interpreter evaluates expressions similar to these.
Continued fractions play an important role in number theory and in approximation theory. In this programming assignment, you will write some short procedures that evaluate continued fractions. There is no predefined code for you to load.
An infinite continued fraction is an expression of the form
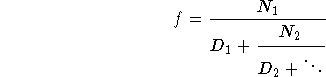
One way to approximate an irrational number is to expand as a continued fraction, and truncate the expansion after a sufficient number of terms. Such a truncation--a so-called k-term finite continued fraction--has the form
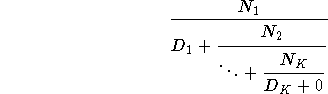
For example, if the 
and the 
are all 1, it is not
hard to show that the infinite continued fraction expansion
converges to 
where 
is the golden ratio
The first few finite continued fraction approximations (also called convergents) are:
and 
of the terms of the continued fraction.
Define procedures cont-frac-r and cont-frac-i such that evaluating (cont-frac-r n d k) and (cont-frac-i n d k) each compute the value of the k-term finite continued fraction. The process that results from applying cont-frac-r should be recursive, and the process that results from applying cont-frac-i should be iterative. Check your procedures by approximating using
(cont-frac (lambda (i) 1)
(lambda (i) 1)
k)
for successive values of k, where cont-frac is cont-frac-r or cont-frac-i. How large must you make k in order to get an approximation that is accurate to 4 decimal places? Turn in a listing of your procedures.
One of the first formulas for was given around 1658 by the English mathematician Lord Brouncker:
This leads to the following procedure for approximating :
(define (estimate-pi k) (/ 4 (+ (brouncker k) 1)))
(define (square x) (* x x))(define (brouncker k) (cont-frac (lambda (i) (square (- (* 2 i) 1))) (lambda (i) 2) k))
where cont-frac is one of your procedures cont-frac-r or cont-frac-i. Use this method to generate approximations to . About how large must you take k in order to get 2 decimal places accuracy? (Don't try for more places unless you are very patient.)
Continued fractions are frequently encountered when approximating
functions. In this case, the and can themselves be
constants or functions of one or more variables. For example, a
continued fraction representation of the inverse tangent function
was published in 1770 by the German mathematician J.H. Lambert:
Verify that your
procedure works (and check its accuracy) by using it to compute the
tangent of a number of arguments, such as 0,
1, 3, 10, 30, 100.
Compare your results with those computed using
Scheme's atan procedure
.
How many terms are required to get reasonable accuracy? Turn in your procedure definition together with some sample results.
The idea of a continued fraction can be generalized to include arbitrary nested expressions such as (1) and (2) below:
or in general
where the are the terms of the expression, the are the arithmetic operators, and R is the residual term (perhaps representing the effects of terms beyond the kth in an approximation). For example, in (2) the are alternately the addition and the multiplication operators, and R=1.
Define a procedure nested-acc such that evaluating (nested-acc op r term k) computes the value of a nested expression. Argument op is a procedure of one argument, that when applied to the term index i returns the ith arithmetic operation (which is a procedure of two arguments). The r argument represents the effect of the R term. Turn in a listing of your procedure.
How would you use your nested-acc procedure to compute a k-term approximation to the function
The Taylor series for computing the sine function is
Define a simple recursive procedure sine-taylor such that (sine-taylor x n) is the sum of the first n terms of the series.
Now verify that your nested-acc procedure works properly by using it to compute the values of this Taylor series and comparing its results to those of sine-taylor.
In certain continued fractions all and terms are equal
and it is convenient to regard the fraction as
being ``built-up'' from a base by a repetitive operation. For
example, given the base function B and the augmentors
N and D, one can build N/(D+B). This can be computed in a
straightforward fashion by the procedure build
(define (build n d b) (/ n (+ d b)))
The value of the expression that is represented by the two-term continued fraction
can then be computed by evaluating (build n d (build n d b)). When further composition is of interest, it is possible to use the repeated procedure defined above.
Write a procedure repeated-build of four arguments k, n, d, and b, which returns a result that is equivalent to applying the build procedure k times. In particular (repeated-build 2 n d b) should return the same result as (build n d (build n d b)). Your implementation of repeated-build should make use of the repeated procedure given above (in a non-trivial way).
Verify that your repeated-build procedure works properly by evaluating the continued fraction for the reciprocal, of the golden ratio:
Now consider the problem of computing the rational functions , , ,
where is the k-th Fibonacci number ().
Making use of your repeated-build procedure, define a procedure r of one argument k that evaluates to a procedure of one argument x that computes . For example, evaluating ((r 2) 0) should return 0.5.
One difficulty with using continued fractions to evaluate functions is that there is generally no way to determine in advance how many terms of an infinite continued fraction are required to achieve a specified degree of accuracy. The result obtained by computing the value of a continued fraction by working backwards from the k-th to the first term cannot generally be used in the computation of the k+1 term continued fraction.
Remarkably, there is a general technique for computing the value of a continued fraction that overcomes this problem. This result is based on the recurrence formulas
It is easy to show that the k-term continued fraction can be computed as
By determining whether is close enough to , it is easy to determine whether to include more terms in the approximation.
Define a procedure that computes the value of a continued fraction using this algorithm. The process that evolves when the procedure is applied should be iterative. Test that your procedure works by computing the tangent of various angles. Use the tracing feature of your SCHEME system to determine how many terms are evaluated.
See Next Page
Turn in this sheet along with your answers to the questions in the problem set:
How much time did you spend on this homework assignment?
We encourage you to work with others on problem sets as long as you acknowledge it (see the 6.001 General Information handout).
If you cooperated with other students, LA's, or others, or found portions of your answers for this problem set in references other than the course text (such as some of the course archives), please indicate your consultants' names and your references in the space below. Also, explicitly label all text and code you are submitting which is the same as that being submitted by one of your coolaborators.
Otherwise, write ``I worked alone using only the course reference materials.'' and sign your statement.
This document was generated using the LaTeX2HTML translator Version 96.1-f (May 31, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 ps2.
The translation was initiated by Jeremy Daniel on Sat Sep 20 16:30:33 EDT 1997