Bayesian Matting

Implementation by Michael Rubinstein

Computational Photography '09, The Interdisciplinary Center Hertzelia

Matting Overview

The purpose of matting is to extract foreground objects from background, often for the purpose of compositing with new environments. A foreground object is extracted from the background by estimating the color and opacity, or alpha channel, for the foreground elements at each pixel. The color value can then be expressed by the composition equation:

where F and B are the foreground and background colors, alpha is the opacity map and C is the resulting color. Therefore, matting can be considered as the inverse process of composition, where we start from a composite image and attempt to extract the foreground and alpha images. This process is typically guided by a user indicating the location of foreground objects.

The Bayesian Approach

This project implements the technique described in [1], where the matting problem is formulated in Bayesian framework, and solved using MAP optimization. In this approach, we search for the most likely estimates of F, B and alpha given C, the observed color. More formally, we optimize

Applying Bayes rule, taking the logarithm and neglecting some terms, this reduces to

where L() denotes the log-probability. Chuang el at. model each of these terms by means of Gaussian distributions (isotropic for the first term, and unisotropic for the second and third), reflecting the spatial distribution of foreground and background colors in the image. As their resulting likelihood equation is not quadratic, it is solved using alternating iterations, until convergence.
To guide the algorithm, a trimap M is required to be given by the user. This map indicates the background regions, foreground regions, and unknown regions. The pixels marked as foreground and background are automatically assigned alpha values 1 and 0 respectively, while the unknown pixels are processed based on the foreground and background information as described above. A high level pseudo code of the algorithm is given below. For further details, see [1] and their project website: http://grail.cs.washington.edu/projects/digital-matting/image-matting/

Implementation Details

  1. As in this approach the pixel neighborhood also considers previously estimated values, the way we traverse the pixels in the unknown regions clearly affects the resulting matte. In our implementation, we process the unknown pixels starting from the boundaries of the unknown regions with the foreground and background regions, iteratively moving toward the inside.
  2. As done in [1], we implemented the top-down clustering method of Orchard and Bouman [2] for partitioning the foreground and background colors. We use the maximal eigenvalue of current nodes as a stop criteria for the splitting process. We also experimented with weighted kmeans clustering, but achieved better results using [2].
  3. We set a parameter for the maximal number of iterations for convergence. Empirically, we found that the likelihood converged within 5-15 iterations on average. During the optimization, we explicitly enforce F, B and alpha to remain in range [0,1].
  4. The camera variance is taken as parameter, default to 0.01. It is also added to the clusters covariance as [1] mention in their addendum.
  5. The pixel neighborhood size should be taken as function of the width of unknown regions in the trimap. It might occur, however, that not enough foreground or background pixels reside within a pixel's neighborhood at a certain iteration of the algorithm. In such case, we postpone the processing of that pixel to later iterations.

The Application

This implementation was developed and tested on MATLAB 7.4.0 (R14). Here are links to the code and images.

The code can be used both from MATLAB command line, or using a simple supplied GUI. A snapshot of the GUI main window is shown below. To run the application, download and extract the code (and images) to some directory and run app.m.
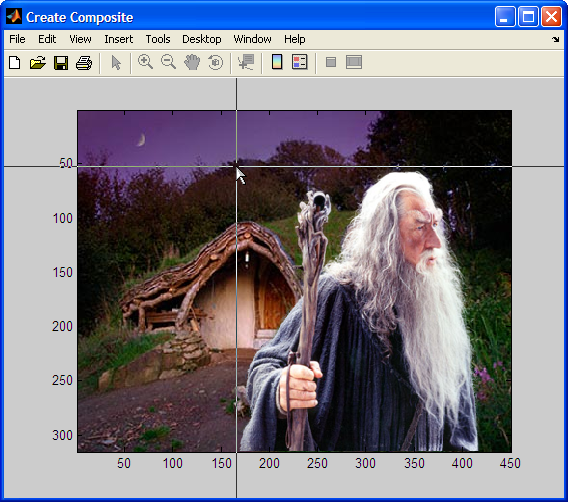
Typical usage will be to first load an image, then supply a trimap (possibly store it for future use), and then run the alpha matting calculation. Once the calculation completes, the foreground can be composed with new backgrounds.
Note that this interface supply a very simple tool for entering the trimap. In practice, we noticed that it might be more convenient for the user to use a professional tool (e.g. Photoshop) for this purpose. From our experiments, finer tuned trimaps might help to achieve better results.

 
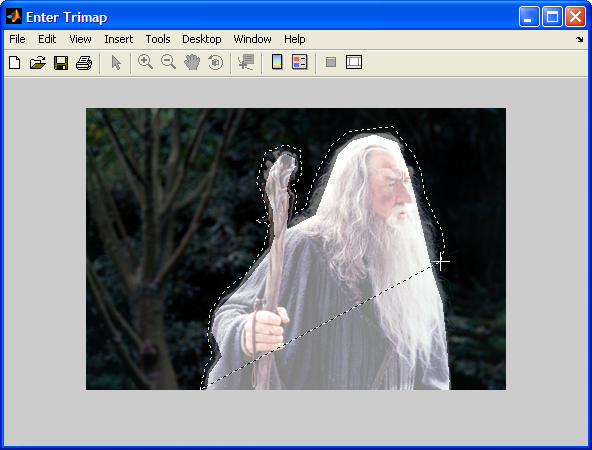Trimap Interface
  
Composition Interface

All parts of the application can be run from MATLAB command line. see script.m for an example which loads an image and trimap, performs the calculation, and generates a composition with a new background. The trimap interface can be called using the function getTrimap.m. The composition interface can be invoked by calling the createComposite.m function. See the documentation and code for further details.

Results

Click on an image to enlarge it.

Sample comparisons to Chuang et al.

Input
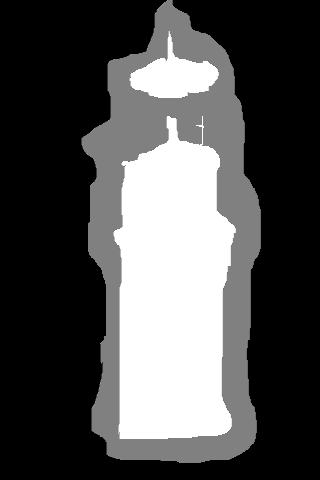
Trimap
Our Result
Chuang
Input
Trimap
Our Result
Chuang

Natural Image Composites

Input
Trimap
New Background
Composite
   
Alpha
Alpha Zoom-in

 


More complicated example

 

References

[1] Yung-Yu Chuang, Brian Curless, David H. Salesin, and Richard Szeliski. A Bayesian Approach to Digital Matting. In Proceedings of IEEE Computer Vision and Pattern Recognition (CVPR 2001), Vol. II, 264-271, December 2001
[2] M. T. Orchard and C. A. Bouman. Color Quantization of Images. In IEEE Transactions on Signal Processing, 39(12):2677–2690, December 1991