Practice Questions
Question
1:
Let
A(n) and B(n) denote the worst-case running time for algorithms A and B,
respectively, as a function of the input size n. Consider the following statements:
I. If A(n) is Theta(B(n)), then B(n) is
Theta(A(n))
II.
If A(n) is O(B(n)), then B(n) is O(A(n))
A.
Statement I is true and Statement II is false
B.
Statement I is false and Statement II is true
C.
Both Statement I and Statement II are true
D.
Both Statement I and Statement II are false
Question
2:
Consider
the following algorithms:
Insertion
sort
Merge
sort
Selection
sort
Bubble
sort
Binary
search
Which
of the following recurrences does NOT describe the worst-case running time of
any of the above algorithms (for an input of size n)?
A.
T(n) = T(n/2) + Theta(1)
B.
T(n) = 2T(n/2) + Theta(n)
C.
T(n) = T(n-1) + Theta(1)
D.
T(n) = T(n-1) + Theta(n)
Question
3:
Consider
a modified version of Merge sort in which the base case of the recursion has
been changed. In the original version, the
base case checked whether the array had one element (or less); if so, it
returned the array without any modifications.
In the new version, the base case checks whether the array has 1000
elements (or less); if so, it sorts those elements using insertion sort and
returns the sorted elements. Given an
array of n elements, what is the worst-case running time of this hybrid sorting
algorithm?
A.
O(n)
B.
O(n log n)
C.
O(n^2)
D.
O(n^2 log n)
Question
4:
Consider
an algorithm that is operating on a sparse graph (that is, a graph with n
vertices and O(n) edges). If the
algorithm changes the representation of matrices from an adjacency list to an
adjacency matrix, which of the following is NOT possible?
A.
The algorithm will run slower.
B.
The algorithm will run faster.
C.
The algorithm will use more space.
D.
The algorithm will use less space.
Question
5:
Suppose
that each edge e of an undirected graph G has a unique positive edge weight
w(e). Suppose T is a Minimum Spanning Tree of G. Consider the following
statements
I.
The heaviest edge in G is an edge in T
II.
The lightest edge in G is an edge in T
A.
Statement I must be true and Statement II must be false
B.
Statement I must be false and Statement II must be true
C.
We cannot say for sure whether Statement I is true
D.
We cannot say for sure whether Statement II is true
Question
6:
Suppose
you are asked to implement a binary search.
The procedure should input an array A of integers, indices hi and lo,
and a value val to search for. It should search the
array elements between A[lo] and A[hi], inclusive. If the value appears in this range, the
procedure should return an index i such that A[i]=x. If the value does not appear in this range,
the procedure should return -1.
Your
friend suggests using the following code:
int
buggy_search(int A[], int lo, int hi, int val) {
int mid = (lo+hi)/2;
if A[mid]==val
return mi
else if lo==hi
return -1
else if (val<A[mid])
return buggy_search(A, lo, mid, val)
else
return buggy_search(A, mid, hi, val)
}
However,
this code has a bug. When an execution
is affected by the bug, what is the program behavior?
A.
It returns -1 when it should have returned a non-negative value
B.
It returns an index i such that A[i]!=x
C.
It causes an infinite recursion (stack overflow error)
D.
It causes an array out-of-bounds exception
Question
7:
Let
f(n) represent the total number of times that QuickSort calls itself
recursively on an array of size n. What
is the tightest upper bound on f(n)?
A.
f(n) = O(log n)
B.
f(n) = O(n)
C.
f(n) = O(n log n)
D.
f(n) = O(n^2)
Question
8:
In
the following procedure, the parameter A represents an unweighted, directed
graph as an adjacency matrix. A[i][j]=1
if and only if there is a directed edge from vertex i to vertex j.
procedure
Mystery(int A[N][N])
for i = 1 to N:
for j = 1 to i:
if A[i][j] == 1 then:
return FALSE
return TRUE
Mystery(A)
returns true if and only if:
A. A represents an acyclic graph.
B. The vertex ordering 1, 2, … N represents a
topological sort of the graph.
C. The graph is not connected.
D. All of the above.
Question
9:
For
which of the following graphs does Prim’s algorithm and Kruskal’s algorithm add
edges to the Minimum Spanning Tree in the same order? Assume that Prim's algorithm starts from
vertex v.
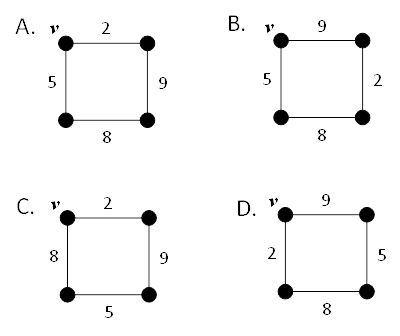
Question
10:
A
group of n students left their shoes outside the classroom. Unfortunately, when they returned the shoes
had been re-arranged. All the shoes are
identical except for the size, which is different for every student and is not
labeled in any way. The only possible
actions are to compare the size of two shoes, to compare the size of two
students' feet, or to test whether a pair of shoes is too big or too small for
a student. What is the worst-case
runtime of the most efficient algorithm for matching every student with their
shoes?
A.
O(n)
B.
O(n log log n)
C.
O(n log n)
D.
O(n^2)
Question
11:
Reconsider
the prior problem, with one small change:
not only have the shoes been reordered, but most of them have been
stolen. In fact, only O(log n) of the
shoes are remaining. Using the same
possible actions as before, what is the worst-case runtime of the most
efficient algorithm for matching the remaining shoes with their owners?
A.
O(n)
B.
O(n log log n)
C.
O(n log n)
D.
O(n^2)
Question
12:
A
courier service delivers packages to a single long street. The houses are numbered in order, from 1 to
n. For convenience, the driver prefers
to park the car and walk to nearby houses whenever possible. However, when the car is parked at a given
house, the driver is only willing to walk up to k houses in either direction. On a given day, let d(i) denote whether a
delivery is required to house i. The
driver wants to deliver all the packages while minimizing the number of parking
locations. What is the best approach?
A.
A dynamic programming algorithm
B.
A greedy algorithm
C.
A sorting algorithm
D.
A binary search algorithm
Question
13:
You
have invented a new mechanical scale that can compare the weight of three items
at a time. After loading the scale, you
can immediately tell which of the three items is the lightest, which is the
heaviest, and which is in between. What
is the best lower bound on the number of three-way comparisons needed to
completely sort n items?
A.
log_2 (n!)
B.
log_3 (n!)
C.
log_6 (n!)
D.
log_10 (n!)
Question
14:
Consider
a weighted, connected undirected graph G, with source vertex s and end vertex
t. Suppose there is a unique shortest
path between s and t, consisting of k edges.
Let x denote the number of edges along this path that also belong to a
Minimum Spanning Tree of G. What is the
tightest correct bound on the value of x?
A.
x = 1
B.
x = k
C.
0 <= x <= k
D.
1 <= x <= k
Question
15:
Consider
a network containing n nodes and m links. If we try to send a packet of data
from some node u along a link to a different node v, the probability that the
packet will be successfully transmitted is p(u, v), where 0 < p(u, v) <
1. Assume that p(u, v) = p(v, u) for all links (u, v) in the network, and that
all failures occur independently of each other. Given this network, and start
vertex s and end vertex t, describe an algorithm to determine the “best” way to
send a packet from s to t, so that the probability that the packet will be
successfully transmitted is as high as possible.