Mixed traffic flow

Numerical simulations of mixed traffic flow with vehicles under car-following and bilateral control.

This webpage contains supplementary material for our paper “On the stability analysis of mixed traffic with vehicles under car-following and bilateral control” submitted to the IEEE Transactions on Automatic Control.

Fig.1: Simulations of pure CFM-traffic (top) and of mixed traffic containing both CFM and BCM vehicles (bottom).

In Fig. 1, black squares denote cars under the constant-time headway car-following model (CFM) control. Red squares denote cars under the bilateral control model (BCM). Circular boundary conditions are used: 32 cars run in a loop. After leaving position 0 on the left they reappear at position 1120 on the right.

For the constant-time headway car-following model (CFM), control is implemented by: $$a_n(t) = k_d\bigl(d_{n}(t)-v_{n}(t)T\bigr)+k_v\bigl(v_{n-1}(t)-v_{n}(t)\bigr).$$ For the bilateral control model (BCM), control is implemented by: $$a_n(t) = \tau k_d\bigl(d_{n}(t)-d_{n+1}(t)\bigr) + \tau k_v\bigl(r_{n}(t)-r_{n+1}(t)\bigr).$$ See section II (in pp. 2) of our paper for a more detailed explanation.

Initially, the cars are spaced equally, 30 meters apart, all moving at a speed of 20 m/sec. Suddenly the car denoted by the solid black square brakes hard at -5 m/sec${}^2$ for 3 sec. After that, constant-time headway CFM is again used to control that car.

See also the MATLAB code used for the above simulation. In the numerical simulation, we set: $$\text{Time step: }\quad \Delta t = 0.1\, \text{sec},$$ $$\text{minimum speed: }\quad V_{\text{min}} = 0\, \text{m/sec},$$ $$\text{maximum speed: }\quad V_{\text{max}} = 44.44\, \text{m/sec} = 160\, \text{km/hour},$$ $$\text{minimum acceleration/deceleration: }\quad a_{\text{min}} = -5\, \text{m/sec}^2,$$ $$\text{maximum acceleration/deceleration: }\quad a_{\text{max}} = +5\, \text{m/sec}^2,$$ $$\text{car length: }\quad \ell = 5\, \text{m}.$$ (in case a collision between car $n$ and car $n+1$ becomes imminent, the speed of car $n+1$ will be set equal to that of car $n$).

The parameters used in the above simulation — also shown in the captions of the subfigures in Fig. 1 — are $$k_d = 0.3\, \text{sec}^{-2}, \quad k_v = 0.2\, \text{sec}^{-1},\quad T = 1.5\, \text{sec}, \quad\text{and}\quad\tau = 1.5.$$ Obviously here $K = 4$ and $L = 4,$ where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

The following two figures (i.e., Fig. 2 and Fi.g. 3) show the trajectories of the cars plotted in the space-time domain. The black curves are trajectories of CFM cars. The red curves are trajectories of BCM cars. The bold black curve corresponds to the trajectory of the solid black square in Fig. 1.

Fig.2: The trajectories of the cars in the pure CFM traffic, corresponding to the top sub-figure in Fig. 1.

Fig.3: The trajectories of the cars in mixed traffic, corresponding to the bottom sub-figure in Fig. 1.

In summary, the stability condition for pure CFM traffic is relaxed by introducing BCM vehicles. In our paper, we provide the detailed mathematical analysis.

The percentage of BCM vehicles in the mixed traffic

The following simulations verify the analysis in our paper. In each case we show a comparison between two situations where one of the parameters is varied. First, we show what happens when the percentage of BCM vehicles in mixed traffic is varied.

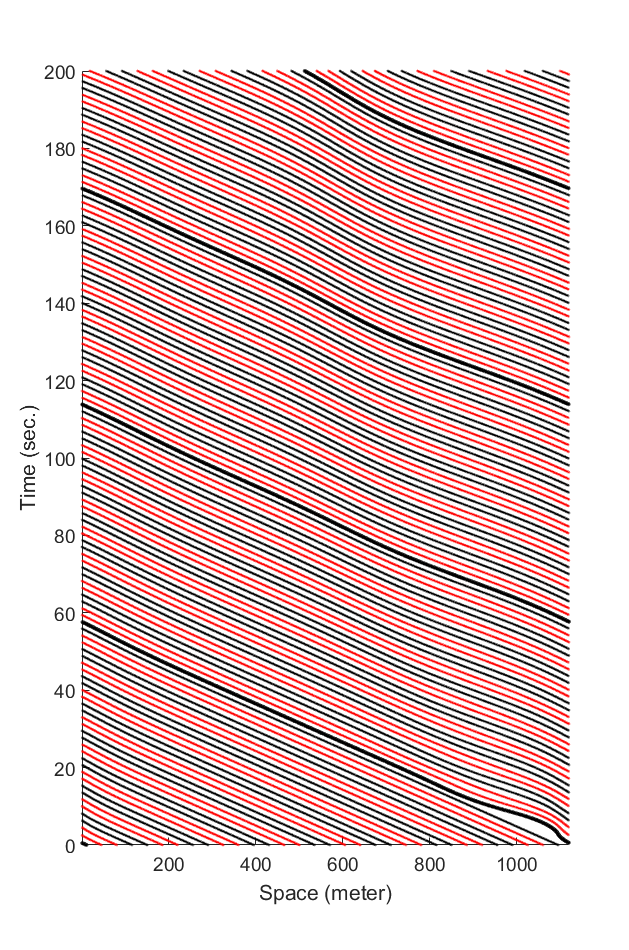
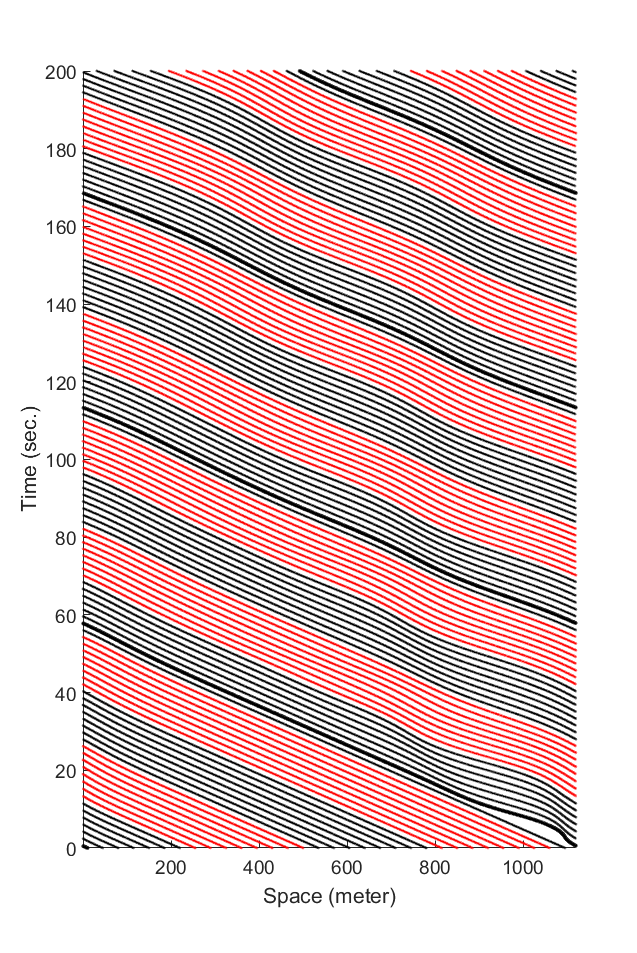
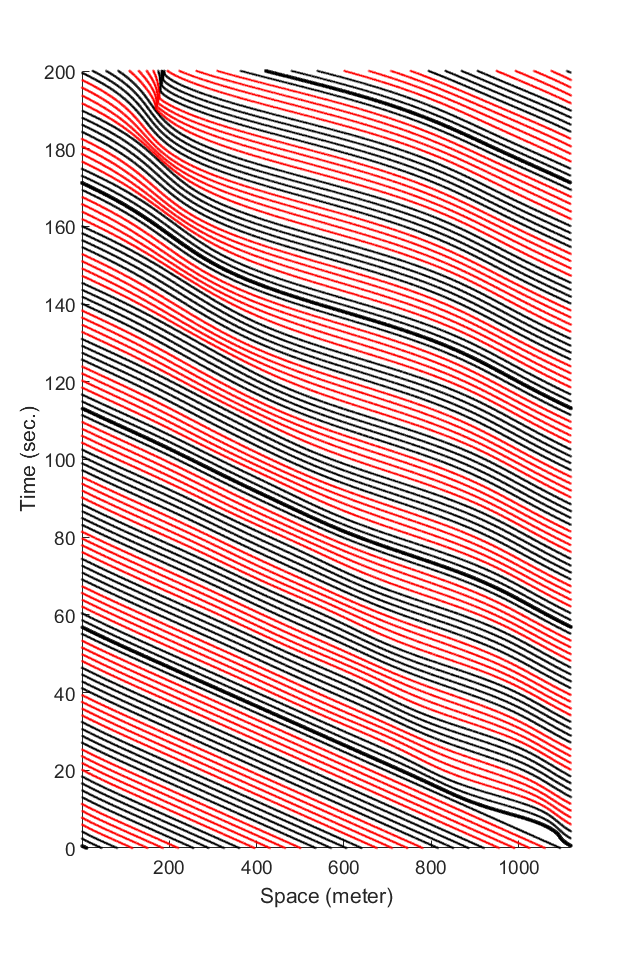
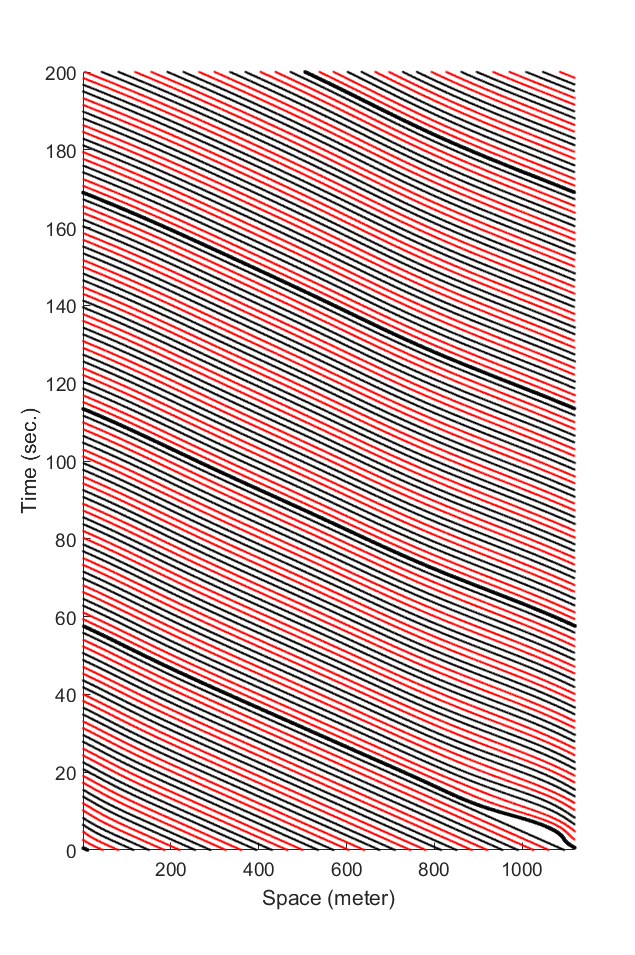
Fig.4: The mixed traffic when $K = 5$ and $L = 3$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

Fig.5: The mixed traffic when $K = 3$ and $L = 5$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

The following two figures (i.e., Fig. 6 and Fig. 7) show the trajectories of cars in mixed traffic shown in Fig. 4 and Fig. 5, respectively.

Fig.6: The trajectories of the cars in the mixed traffic in Fig. 4, corresponding to the bottom sub-figure in Fig. 4..

Fig.7: The trajectories of the cars in the mixed traffic in Fig. 5, corresponding to the bottom sub-figure in Fig. 5.

The following two simulations show two more extreme cases for comparison.

Fig.8: The mixed traffic when $K = 6$ and $L = 2$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

Fig.9: The mixed traffic when $K = 2$ and $L = 6$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

The following two figures (i.e., Fig. 10 and Fig. 11) show the trajectories of cars in the mixed traffic situations shown in Fig. 8 and Fig. 9, respectively.

Fig.10: The trajectories of the cars in the mixed traffic situation shown in Fig. 8, corresponding to the bottom sub-figure in Fig. 8..

Fig.11: The trajectories of the cars in the mixed traffic situation in Fig. 9, corresponding to the bottom sub-figure in Fig. 9.

The distribution of BCM cars (i.e., concentrated or dispersed).

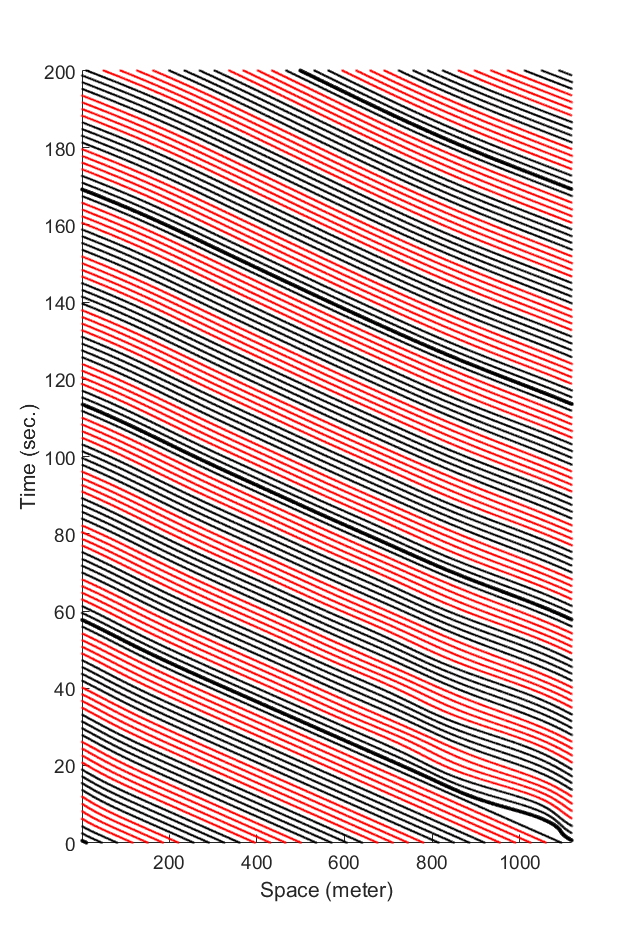
Here we show the effects when the distribution of BCM vehicles in mixed traffic is varied. (In each case, the percentage of BCM vehicles is fixed at 50%.)

Fig.12: The mixed traffic when $K = 2$ and $L = 2$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

Fig.13: The mixed traffic when $K = 8$ and $L = 8$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

The following two figures (i.e., Fig. 14 and Fig. 15) show the trajectories of cars in the mixed traffic shown in Fig. 12 and Fig. 13, respectively.

Fig.14 The trajectories of the cars in the mixed traffic in Fig. 12, corresponding to the bottom sub-figure in Fig. 12..

Fig.15: The trajectories of the cars in the mixed traffic in Fig. 13, corresponding to the bottom sub-figure in Fig. 13.

The parameter $\tau$.

Here we show simulations with various values for $\tau$. These simulations also verify the analysis in our paper.

Fig.16: The mixed traffic when $\tau$ = 0.8. We choose $K = 4$ and $L = 4$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

Fig.17: The mixed traffic when $\tau$ = 2. We choose $K = 2$ and $L = 2$, where $K$ denotes the number of cars in each CFM chain and $L$ denotes the number of cars in each BCM chain.

The following two figures (i.e., Fig. 18 and Fig. 19) shows the trajectories of cars in the mixed traffic shown in Fig. 16 and Fig. 17, respectively.

Fig.18 The trajectories of the cars in the mixed traffic in Fig. 16, corresponding to the bottom sub-figure in Fig. 16..

Fig.19: The trajectories of the cars in the mixed traffic in Fig. 17, corresponding to the bottom sub-figure in Fig. 17.

In order to see the effect of using various values of $\tau$, first, please compare the simulation in Fig. 1 with the simulation in Fig. 16 (and correspondingly the trajectories shown in Fig. 3 with the trajectories shown in Fig. 18). The same conclusion can be found by comparing the simulation in Fig. 12 with the simulation in Fig. 17 (and correspondingly the trajectories shown in Fig. 14 with the trajectories shown in Fig. 19).

Basically, as $\tau$ increases, the stability condition can be relaxed more and more. See our paper for detailed mathematical analysis.

In summary, the above numerical simulations verify the theoretical analysis in our paper.

The corresponding MATLAB code

The above simulations are produced by the MATLAB code. The parameters can be changed by changing the first few lines of code.

Numerical simulations of mixed traffic flow with vehicles under car-following and bilateral control.

The percentage of BCM vehicles in the mixed traffic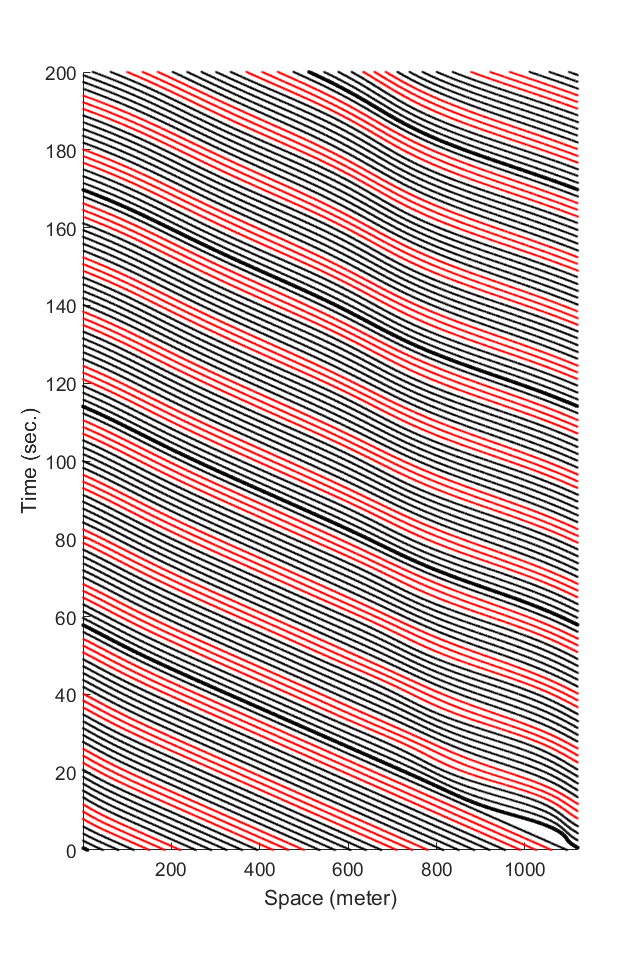

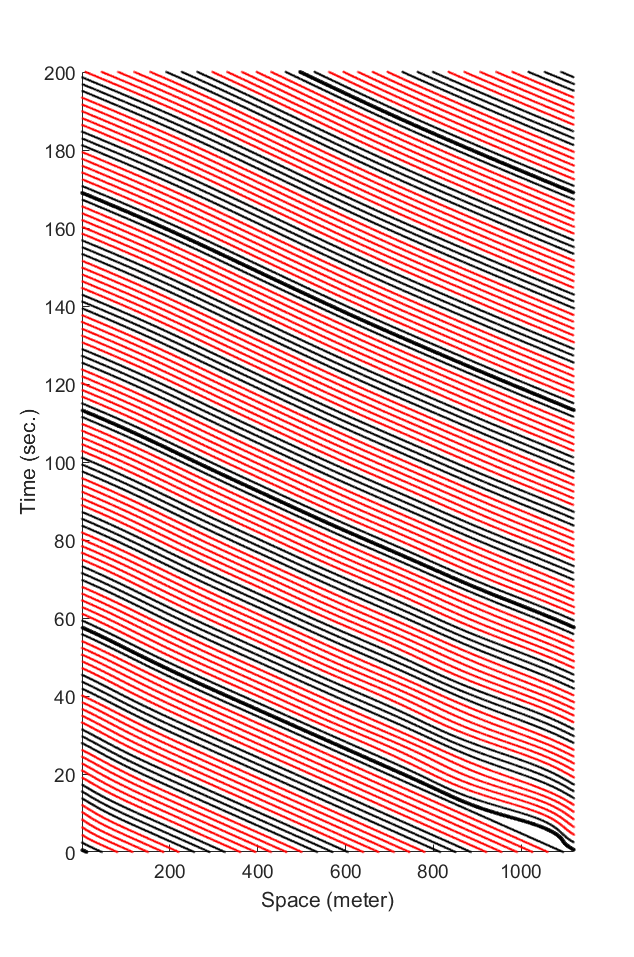
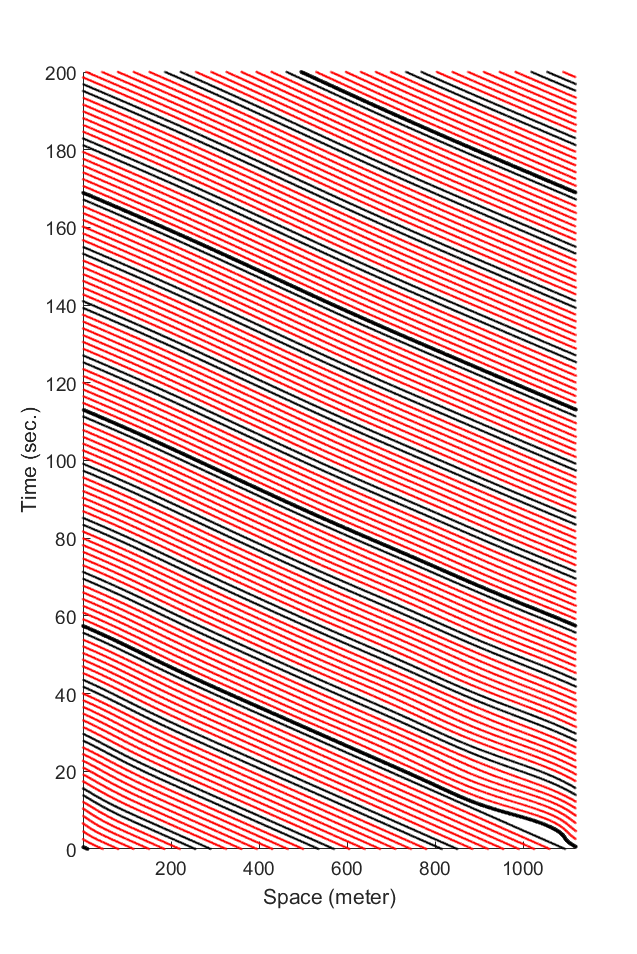
The distribution of BCM cars (i.e., concentrated or dispersed).

The parameter \(\tau\).

The corresponding MATLAB code