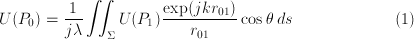
This is a great book on optics:
Goodman, Joseph W. Introduction to Fourier Optics. Roberts & Company Publishers, 2005.
Page numbers below refer to pages in this book.
We want to calculate the scalar field created by light coming through an aperture. The scalar field is a complex-valued scalar function over space that captures the necessary information about propagating light, given certain assumptions (p. 35).
The Huygens-Fresnel principle says that the field at a point can be calculated by summing contributions from spherical waves emanating from each point in the aperture. Mathematically (p. 52):
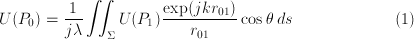
where:
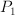is a point in the aperture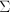 
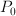is the point where we wish to calculate the field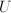 
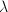is the wavelength of the incoming (monochromatic) light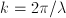
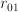is the distance between 
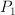and 
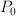
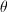is the angle made with the aperture normal by the ray from 
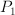to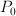 
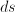is an infinitesimal area element of the aperture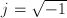
A faster way to do calculations on propagating light is to decompose
the scalar field into plane-waves propagating in different directions.
When an x-y slice of such a plane-wave is viewed, it will have a
frequency between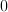 
and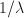 
.
Writing the field in terms of its x-y Fourier transform (p. 60):
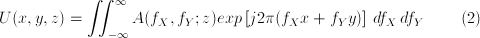
The transfer function for propagating waves across a distance 
in
Fourier space is then (p. 61):
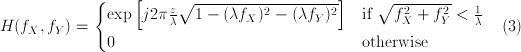
Note that the angular spectrum approach and the Rayleigh-Sommerfeld integral yield identical predictions of the diffracted field (p. 61).
A lens simply introduces a phase factor proportional to its thickness
at a given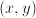 
position on its plane. In the paraxial
approximation (rays close to parallel with the optical axis) it can be
written (p. 101):
![<code>expleft[-jfrack2f(x^2+y^2)right]</code>](diffraction-images/diffraction22.png)
where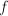 
is the focal distance. Note that the refractive index of
the lens is not needed, as it is included in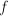 
. Goodman
introduces 
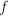after making the paraxial approximation, but by
undoing the small-angle approximation we get the presumably more
accurate:
![<code>expleft[-jkleft(f-sqrtf^2-x^2-y^2right)right]</code>](diffraction-images/diffraction26.png)
To calculate the diffraction pattern created on the film by a plane wave incident on an aperture containing a lens:
Choose a set of x-y values (or just x-values, neglecting y to get a 1-D pattern) spaced no closer than half a wavelength; spacing them farther apart seems to work, to a point; the values need not extend beyond the aperture in magnitude
Calculate the scalar field in the plane of the aperture by evaluating the plane wave, which represents an infinitely distant point source; points not in the aperture are set to 0
Apply the phase shift from the lens
Perform an FFT to work in angular spectrum space; make sure you know what signed frequency each element of the result represents
To propagate by some z-distance, apply the propagation phase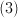 
in Fourier space
To apply an occluding mask, perform an IFFT followed by a binary mask followed by an FFT
You may then propagate again, mask again, etc.
When you get to the film plane, perform an IFFT and take the squared magnitude to get the intensity pattern on the film
This intensity pattern is the point response to the distant source; assuming your distant sources are incoherent, the intensity patterns add linearly, and the pattern on the film is linear in the intensities of the sources (p. 135)