Iterative Reweighted Least Squares

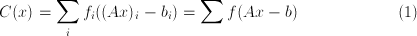
I was shown this technique by Anat Levin, who pointed me to the paper "User assisted separation of reflections from a single image using a sparsity prior" by Anat Levin and Yair Weiss as an example of how the method is used. I subsequently "reverse-engineered" the method a bit to get an idea for what it does.

IRLS minimizes the cost function:

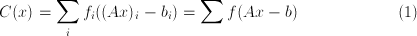
where my notation is:

lowercase variables are vectors by default
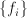the functions are scalar potential functions that are smallest at 0
an unindexed sum is performed over the elements of its vector argument

The intuitive explanation of the method is that each potential function is approximated at each iteration by a parabola through the origin that has the correct slope at the current value of <code>x</code> being considered.

Derivation

Taking the derivative of the cost function:

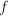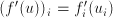where the derivative of <code>f</code> is taken element-wise ( <code>(f(u))_i = f_i(u_i)</code> ).

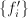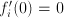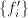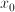If all the potentials were parabolas we could do least-squares. In this case, all the <code>f_i</code> would be linear. Taking into account that <code>f_i(0)=0</code> , we can approximate the functions as linear based on the current value of <code>x</code> (denoted <code>x_0</code> ), as follows:

$<code>C(x) approx A^T left[ (Ax-b) ast fracf(Ax_0-b)Ax_0-bright]</code>$

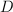where <code>ast</code> denotes element-wise multiplication and the fraction bar denotes element-wise division. Defining a diagonal matrix <code>D</code> for the weights, we want the derivative of the cost function to vanish:

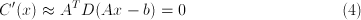
<code>C(x) approx A^T D (Ax-b) = 0</code>

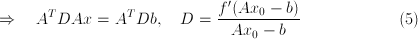
$<code>Rightarrow quad A^T D A x = A^T D b quad D = fracf(Ax_0-b)A</code>$

This is the least-squares problem we solve at each iteration to get the new value <code>x</code> from the old value 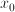<code>x_0</code> .

Example: Reconstruction with a sparse wavelet prior

Suppose we wish to minimize the following cost function for <code>x</code> :

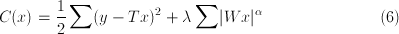
$<code>C(x) = frac12sum(y-Tx)^2 + lambda sum lvert Wx rvert^alpha</code>$

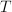where we wish to recover an image <code>x</code> that has been transformed by a known transformation <code>T</code> to yield a noisy observation 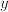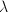<code>y</code> , <code>lambda</code> is some positive scalar weight, 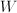<code>W</code> takes into a wavelet basis, and the absolute value and exponentiation are performed element-wise.

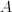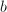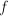We define <code>A</code> , <code>b</code> , and <code>f</code> for this problem:

<code>A = left[ c T W right] quad b = left[ c y 0 right]</code>

<code>f(Ax-b) = fleft(left[c Tx-y Wx right] right) = left[ c (Tx-</code>

and calculate the weights:

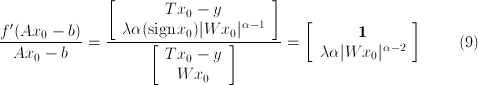
$<code>fracf(Ax_0-b)Ax_0-b = fracleft[ c Tx_0-y lambdaalpha(textsi</code>$

where 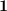<code>mathbf1</code> is a vector consisting of the appropriate number of ones. Writing out the diagonal matrix for the weights:

<code>D = left[cc I 0 0 Psi right] quad Psi = textdiagleft(lambda</code>

Remember that at each iteration we solve:

where 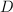<code>D</code> incorporates information from the previous iteration. In this example, the equation becomes:

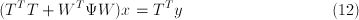
This works well when implemented.

Some tips:

Don't raise small or zero numbers to negative powers, set a lower bound (e.g. 1e-4)
If your prior is nonlinear, pay attention to the units of
Convergence happens after a small number of iterations, typically fewer than 10
For image reconstruction with a convex prior (e.g. L1), the result is quite close to the exact global optimum and looks at least as good visually
Use sparse matrices when possible, of course

Back

View texdown source