Presentation of Theoretical Computer Science and PCP

By Dana Moshkovitz

 

On May 6th 2007 (LAG BA’OMER), we had a Science Day at the Weizmann Institute.

 

I was asked to present my research in this event for laypersons. Here’s the outcome:

 

[LOGO][LOGO][LOGO]

 

 

Where Are We?

 

I tried to sketch a map that would explain where we are inside the area of Computer Science.

 

Roughly speaking, we can partition Computer Science (CS) into Theoretical CS and Applied CS.

 

In Applied CS you can find sub-areas such as Software Engineering and Networks, and you can find applications of CS to other fields, such as biology.

 

We’re in Theoretical CS. This is the branch of Pure Mathematics that studies the nature of problem solving, or computing. We can further divide this area as follows:

 

 

 

 

Theoretical Computer Science

 

·         Algorithms solve problems efficiently: with as few operations, as little memory usage memory, as little usage of randomness, etc.

 

·         Complexity tries to understand the limits of algorithms: how many operations are needed? how much memory usage? how much randomness? etc.

The P vs. NP Question and Mathematics

 

In plain English the P vs. NP question means: is solving a problem as easy as checking a solution?

 

Whether P=NP or not is the fundamental open problem of Complexity Theory and Theoretical Computer Science. It is recognized as one of the most important open problems in Mathematics.

 

The reason that it is so important to Math is that it is a question about the very foundations of Mathematics: Is there an efficient algorithm for theorem proving?

 

To understand more the fundamental nature of this problem and Complexity in general, look at this survey by Avi Wigderson.

 

In the presentation I try to explain the P vs. NP question and sketch how our field evolved with respect to it.

 

 

 

Complexity, Sudoku and Real Life Problems

 

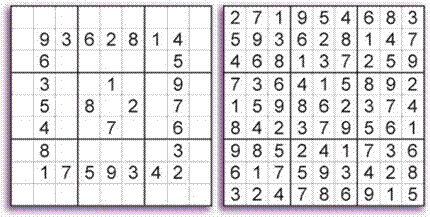
As an example for an algorithmic problem I use Sudoku on n´n tables (this means that I don’t want to restrict myself to the standard 9´9 tables; I want to look on the general problem).

 

Sudoku has the interesting property that given a solution, anyone can easily check it (even if they can’t solve the Sudoku themselves). Checking merely involves summing up the numbers on the rows/columns/boxes of the Sudoku table.

 

The fundamental Theorem of Complexity (Cook-Levin-Karp, 1972) implies that Sudoku is (computationally) equivalent to a huge variety of (much more) important problems.

 

Among these important problems one can find problems in design of networks (“networks” can be computer networks or train networks, for example), finding interesting sub-structures (e.g., in DNA), etc.

 

The equivalence between Sudoku and all these problems means that:

there is an efficient algorithm that solves any Sudoku table if and only if there is an efficient algorithm to any one of these problems.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

My Research: PCP

 

I work on PCP, which is shorthand for Probabilistically Checkable Proofs.

 

The PCP Theorem (Arora-Safra-Lund-Motwani-Sudan-Szegedy, 1992) states that one can write any solution for a Sudoku riddle in a way that allows extremely fast probabilistic checking:

 

1.   Pick at random a constant number of places in the new solution (say 2 places).

2.   Check only them.

 

If my solution is ok, no matter which places you pick, everything will look ok.

 

However, if I don’t have a solution, then no matter what I write, the probability that things will look ok to you is small, say 0.1%.

 

This is very surprising, given that in order to check standard Sudoku solutions, one essentially has to read the entire solution.

 

Indeed, the new way(s) to write the Sudoku solution so that it can be verified so easily are very clever. They involve many ideas of many researchers, starting from the mid-1980’s and to this day. And they use tools from all over Mathematics: Algebra, Analysis, Combinatorics, Graph Theory and Coding Theory.

 

Implications.

 

Interestingly, by an observation first made by Feige-Goldwasser-Lovász-Safra-Szegedy in 1991, the PCP Theorem has more far-reaching consequences!

 

The PCP Theorem implies the impossibility (assuming P≠NP) to efficiently approximate (to within appropriate factors), given a Sudoku table, the maximal number of rows/columns/boxes that a solution can satisfy.

 

The PCP Theorem also implies that, assuming P≠NP, almost all the aforementioned “much-more-important-problems” (about network design, DNA sub-structures etc) don’t even have efficient approximation algorithms!