max van kleek
6.869 advances in computer vision: learning and interfaces
problem set two
march 10, 2005
problem one
part one a)
the difference-of-gaussian is a function DoG(x, y, sigma, k) where:
- x,y - x,y-coord of point to be evaluated
- sigma - base standard deviation of the gaussian
- k - multiplicative factor for sigma to get the sigma for the next-level gaussian
or, equivalently could be defined as DoG(x, y, sigma1, sigma2):
- x,y - x,y-coord of point to be evaluated
- sigma1 - base standard deviation of the first gaussian
- sigma2 - base standard deviation of the second gaussian
part one b)
to speed up scale selection, the paper does two things:
- iterative blurring of layers
- Instead of blurring each layer with the appropriate (k^n)*sigma,
which would require a large gaussian (blur) kernel and thus would
be computationally expensive, we perform an iterative blurring,
taking the image at a particular blur and convolving it with sigma_delta
(defined next) to yield the next level. Sigma_delta is effectively much
smaller than (k^n)*sigma, therefore the convolution is efficient.
- downsampling every octave
- Instead of generating the image layers used to make DoG layers at all scales,
the paper only generates image layers corresponding to the levels between a
given sigma to twice that sigma. Then, to generate the next (and successive)
octaves, the existing image layer generated for the current octave corresponding
to 2*sigma is downsampled to half its original resolution - a very fast operation,
and the process repeated.
part one c)
Using the gaussian semi-group property we want to find an expression for g(sigma_delta):
- g(sigma_delta^2) * (g(sigma_cur^2) * I) = g((k*sigma_cur)^2) * I
- setup: We want to find a sigma_delta which we can convolve with
an image blurred with a gaussian of variance (sigma_cur^2) to
get an image blurred at k^2 * sigma_cur^2.
- g(sigma_delta^2) * (g(sigma_cur^2) * I) = g((k*sigma_cur)^2) * I
- convolution is associative!
- g(sigma_delta^2 + sigma_cur^2) * I = g((k*sigma_cur)^2) * I
- use semi-group property
- sigma_delta^2 + sigma_cur^2 = (k*sigma_cur)^2
- now we can concentrate on the inside
- sigma_delta = sqrt((k*sigma_cur)^2 - sigma_cur^2)
- isolating terms..
- sigma_delta = sigma_cur*sqrt(k^2 - 1)
keypoint detector code:
compute_dog_points
function Points = compute_dog_points(Image)
%% computes difference-of-gaussian keypoints on Image
function sd = sigmadelta(k,sigma_cur)
%% returns the sigma_delta (what we need to convolve with to
%% achieve an blur of k more than sigma_cur
sd = sigma_cur*sqrt(k.^2-1);
end;
%% retrieves parameters from get_dog_params
%% first scales up image, and blurs it to initial sigma
[InitSigma,Scales,PeakThresh,R] = get_dog_params;
%% first upsample by 2
Image = imresize(Image, [2*size(Image,1) 2*size(Image,2)]);
% then blur to initial sigma
sprintf('blurring initial image by %d',sigmadelta(1.6,1.0))
initial_image = blurGauss(Image,sigmadelta(1.6,1.0));
% figure out realistically the # of octaves we want to do
n_octaves = floor(log2(min(size(Image))-10)) - 5
Points = [];
cur_octave = initial_image;
osize = 0.5;
for octave=1:n_octaves,
[p cur_octave] = process_octave(cur_octave,osize);
Points = [Points; p];
osize = osize/2;
end
end
process_octave
% [P,nextOctave] = process_octave(Octave,octSize)
% takes Octave and first downsamples it by 2 to render it half its
% original size. then generates images at gaussians of successive
% multiples of k=2.^(1/S) and computes Difference-of-Gaussians,
% finding and collecting extrema along the way. Calls
% find_dog_peaks and scales resulting points back to their
% positions on the original image.
function [P,nextOctave] = process_octave(Octave,octSize)
function sd = sigmadelta(k,sigma_cur)
%% returns the sigma_delta (what we need to convolve with to
%% achieve an blur of k more than sigma_cur
sd = sigma_cur*sqrt(k.^2-1);
end;
function img = downsampleImageByTwo(Image)
% downsamples Image by 2 in each direction
img = downsample(downsample(Image,2)',2)';
end;
P = [];
%% get parameters
[InitSigma,Scales,PeakThresh,R] = get_dog_params;
k = 2.^(1/Scales);
% compute our current "sigma" based upon passed in octSize
% ie,
% octsize = 0.5, then sigma = 1/(2*0.5) = 1.0 * InitSigma;
% octsize = 0.25 then sigma = 1/(2*0.25) = 2*InitSigma
%% Confusion
%% I was quite confused here. I was not sure whether we wanted
%% to re-compute the sigma relative to the previous octave, or whether we
%% essentially "started over" with InitSigma; OR, if we wanted to
%% set our starting sigma to 1.0 for all but the first octave...
sigma_cur = InitSigma;
%% to create base sublevel,
%% downsample incoming Octave image to 1/2 size
sublevel = downsampleImageByTwo(Octave);
sublevels(:,:,1) = sublevel;
%% first generate image levels
for sublevel_i = 2:Scales+3,
% using incremental sigma
sublevels(:,:,sublevel_i) = ...
blurGauss(sublevel,sigmadelta(k,sigma_cur));
sublevel = sublevels(:,:,sublevel_i);
sigma_cur = k*sigma_cur;
end;
%% compute difference of gaussians (DOG)s for this octave
for dog_i = 1:Scales+2,
dogs(:,:,dog_i) = sublevels(:,:,dog_i + 1) ...
- sublevels(:,:,dog_i);
end;
P = find_dog_peaks(dogs,octSize);
nextOctave = sublevels(:,:,Scales+1);
end
find_dog_peaks
% P = find_dog_peaks(DoG, octSize)
% searches a set of DoG levels for keypoints and returns a
% list of such keypoints, scaled (using octSize) back to the
% positions on the original image.
function P = find_dog_peaks(DoG, octSize)
Points = [];
PERIM_MARGIN = 5;
%% get parameters
[InitSigma,Scales,PeakThresh,R] = get_dog_params;
for dog_level = 2:size(DoG,3)-1,
for i=PERIM_MARGIN:size(DoG,1)-PERIM_MARGIN,
for j=PERIM_MARGIN:size(DoG,2)-PERIM_MARGIN,
% extract a 3x3x3 neighborhood patch from the DOG pyramid
patch = DoG([i-1:i+1],[j-1:j+1],[dog_level-1:dog_level+1]);
if ( (patch(2,2,2) > PeakThresh/Scales) && ...
is_local_extremum(patch) && ...
not_an_edge(DoG,i,j,R))
% it's a keypoint!
k=2^(1/Scales);
sigma_cur = (1/octSize)*InitSigma*k.^(dog_level-1);
Points = [Points; [i j sigma_cur]];
end;
end;
end;
%% rescale image points back to positions in original image
P = (1/octSize)*Points;
end;
is_local_extremum
% A = is_local_extremum(N)
% takes a 3x3x3 neighbourhood from a DoG and
% determines whether the center pixels is an
% extremum (local min or max); returns 1 (true)
% or 0 (false) accordingly.
function A = is_local_extremum(N)
A = 0;
[m i] = max(N(:));
if i == 14 && sum(N(:)==m)==1,
A = 1;
end
[m i] = min(N(:));
if i == 14 && sum(N(:)==m)==1,
A = 1;
end
not_an_edge
% A = not_an_edge(DoG,row,col,R)
% computes the hessian to determine whether or not row,col is along
% an edge.
% row >= 2
% col >= 2
% row <= size(DoG,1)
function [A,eigen_vectorz] = not_an_edge(DoG, row, col, R, w)
if (~exist('w')),
w = 3;
end;
halfw = floor(w/2);
patch = DoG([row-halfw:row+halfw],[col-halfw:col+halfw]);
a = diff(patch,2,2);
dXdX = mean(sum(a,2)/w);
a = diff(patch,2,1);
dYdY = mean(sum(a,1)/w);
a = diff(diff(patch,1,1),1,2);
dXdY = mean(a(:));
H = [dXdX dXdY; dXdY dYdY];
A = 0;
[v d] = eig(H);
eigen_vectorz = v;
eigval=diag(d);
if eigval(1) ~= 0 && eigval(2) ~= 0 && det(H) > 0 ...
&& eigval(1)/eigval(2) < R,
A = 1;
end;
blurGauss
% IM = blurGauss(Im, sigma)
% returns Im convolved with a 2D gaussian with stdev sigma
function IM = blurGauss(Im, sigma)
stdev_cutoff = 4.0; %% cutoff for # of standard deviations
g = mkGaussian(ceil(stdev_cutoff*2.0*sigma - 1), sigma.^2);
IM = rconv2(g,Im);
get_dog_params
function [InitSigma,Scales,PeakThresh,R] = get_dog_params()
InitSigma = 1.6;
Scales = 3;
PeakThresh = 0.08;
R = 10;
problem one - part two a)
results of running einstein with PeakThresh=0.03, InitSigma=1.6, Slices=3, R=10 for 3 octaves:
 |
53 points:
x coord y coord sigma
----------------------------
24.0000 52.0000 10.1594
48.0000 52.0000 10.1594
96.0000 218.0000 10.1594
102.0000 52.0000 10.1594
104.0000 84.0000 10.1594
132.0000 52.0000 10.1594
134.0000 98.0000 10.1594
186.0000 100.0000 10.1594
188.0000 240.0000 10.1594
208.0000 390.0000 10.1594
210.0000 264.0000 10.1594
218.0000 242.0000 10.1594
226.0000 58.0000 10.1594
264.0000 98.0000 10.1594
270.0000 266.0000 10.1594
334.0000 286.0000 10.1594
382.0000 308.0000 10.1594
418.0000 318.0000 10.1594
428.0000 52.0000 10.1594
430.0000 316.0000 10.1594
464.0000 150.0000 10.1594
476.0000 20.0000 10.1594
482.0000 292.0000 10.1594
484.0000 332.0000 10.1594
36.0000 428.0000 12.8000
38.0000 276.0000 12.8000
92.0000 428.0000 12.8000
218.0000 370.0000 12.8000
|
einstein.jpg - results of running einstein with PeakThresh=0.08, InitSigma=1.6, Slices=3, R=10 for 3 octaves:
 |
15 points:
x coord y coord sigma
----------------------------
194.0000 226.0000 10.1594
224.0000 180.0000 10.1594
270.0000 266.0000 10.1594
272.0000 286.0000 10.1594
334.0000 286.0000 10.1594
382.0000 308.0000 10.1594
476.0000 20.0000 10.1594
192.0000 364.0000 12.8000
252.0000 350.0000 12.8000
268.0000 232.0000 12.8000
362.0000 276.0000 12.8000
272.0000 268.0000 40.6375
328.0000 292.0000 40.6375
256.0000 344.0000 51.2000
308.0000 220.0000 51.2000
220.0000 330.0000 12.8000
244.0000 190.0000 12.8000
252.0000 350.0000 12.8000
254.0000 78.0000 12.8000
260.0000 406.0000 12.8000
262.0000 144.0000 12.8000
|
x coord y coord sigma
----------------------------
268.0000 232.0000 12.8000
278.0000 78.0000 12.8000
428.0000 494.0000 12.8000
80.0000 92.0000 40.6375
96.0000 52.0000 40.6375
192.0000 296.0000 40.6375
220.0000 388.0000 40.6375
244.0000 200.0000 40.6375
272.0000 264.0000 40.6375
328.0000 292.0000 40.6375
52.0000 280.0000 51.2000
132.0000 384.0000 51.2000
256.0000 344.0000 51.2000
260.0000 252.0000 51.2000
372.0000 292.0000 51.2000
336.0000 248.0000 162.5499
376.0000 88.0000 162.5499
256.0000 360.0000 204.8000
312.0000 224.0000 204.8000
|
problem one - part two b)
einstein05:
 |
12 points:
x coord y coord sigma
----------------------------
194.0000 226.0000 10.1594
224.0000 180.0000 10.1594
272.0000 286.0000 10.1594
334.0000 286.0000 10.1594
382.0000 308.0000 10.1594
474.0000 22.0000 10.1594
170.0000 278.0000 12.8000
324.0000 334.0000 12.8000
362.0000 276.0000 12.8000
272.0000 264.0000 40.6375
328.0000 292.0000 40.6375
256.0000 344.0000 51.2000
|
einstein06.jpg:
 |
15 points:
x coord y coord sigma
----------------------------
206.0000 352.0000 10.1594
224.0000 180.0000 10.1594
270.0000 266.0000 10.1594
272.0000 286.0000 10.1594
274.0000 240.0000 10.1594
320.0000 310.0000 10.1594
334.0000 288.0000 10.1594
370.0000 52.0000 10.1594
474.0000 22.0000 10.1594
192.0000 362.0000 12.8000
244.0000 258.0000 12.8000
250.0000 350.0000 12.8000
326.0000 332.0000 12.8000
272.0000 268.0000 40.6375
328.0000 292.0000 40.6375
372.0000 292.0000 51.2000
|
einstein07.jpg
 |
15 points:
x coord y coord sigma
----------------------------
194.0000 226.0000 10.1594
200.0000 184.0000 10.1594
206.0000 352.0000 10.1594
224.0000 180.0000 10.1594
334.0000 286.0000 10.1594
382.0000 308.0000 10.1594
476.0000 20.0000 10.1594
192.0000 364.0000 12.8000
268.0000 232.0000 12.8000
324.0000 334.0000 12.8000
362.0000 276.0000 12.8000
416.0000 290.0000 12.8000
272.0000 264.0000 40.6375
328.0000 292.0000 40.6375
256.0000 344.0000 51.2000
|
einstein08.jpg
 |
16 points:
x coord y coord sigma
----------------------------
194.0000 226.0000 10.1594
200.0000 184.0000 10.1594
206.0000 352.0000 10.1594
224.0000 180.0000 10.1594
272.0000 286.0000 10.1594
274.0000 276.0000 10.1594
334.0000 286.0000 10.1594
382.0000 308.0000 10.1594
170.0000 278.0000 12.8000
326.0000 334.0000 12.8000
362.0000 276.0000 12.8000
416.0000 290.0000 12.8000
272.0000 268.0000 40.6375
328.0000 292.0000 40.6375
256.0000 344.0000 51.2000
308.0000 220.0000 51.2000
|
einstein-09.jpg
 |
13 points:
x coord y coord sigma
----------------------------
194.0000 226.0000 10.1594
272.0000 288.0000 10.1594
334.0000 286.0000 10.1594
380.0000 310.0000 10.1594
476.0000 20.0000 10.1594
268.0000 232.0000 12.8000
326.0000 332.0000 12.8000
362.0000 276.0000 12.8000
416.0000 288.0000 12.8000
272.0000 268.0000 40.6375
328.0000 292.0000 40.6375
256.0000 344.0000 51.2000
308.0000 224.0000 51.2000
|
problem one part two c)
problem one part two d)
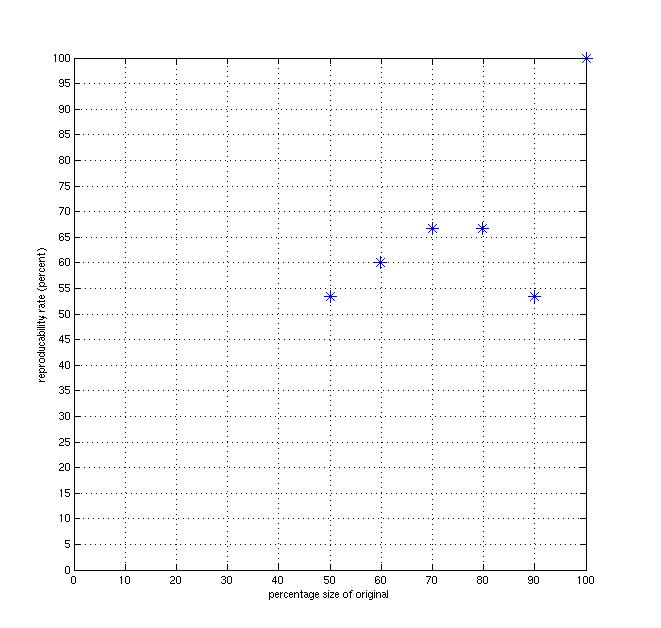
The following is a plot of just the recognition rates for
keypoints when the number of intermediate scales [2, 3, 4, 5],
as a function of how large the image is (ie, which einstein we chose).
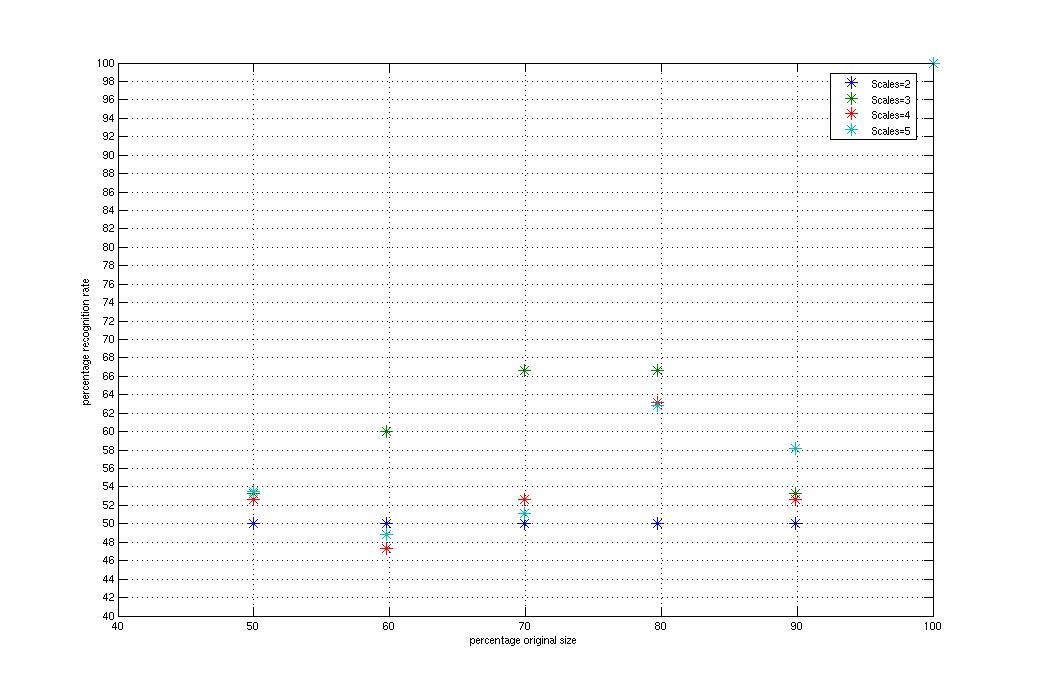
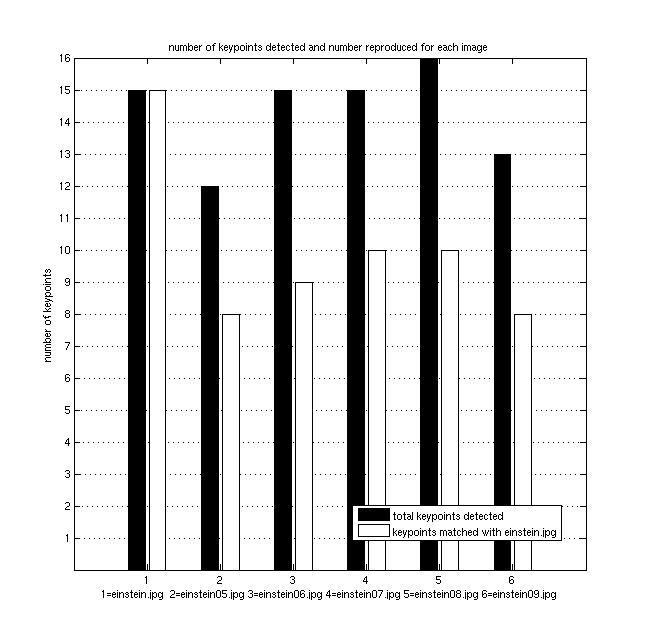
The following is a plot comparing the number of keypoints found when the
number of scales is set to each of 2, 3, 4 and 5 verus the number later
identified.
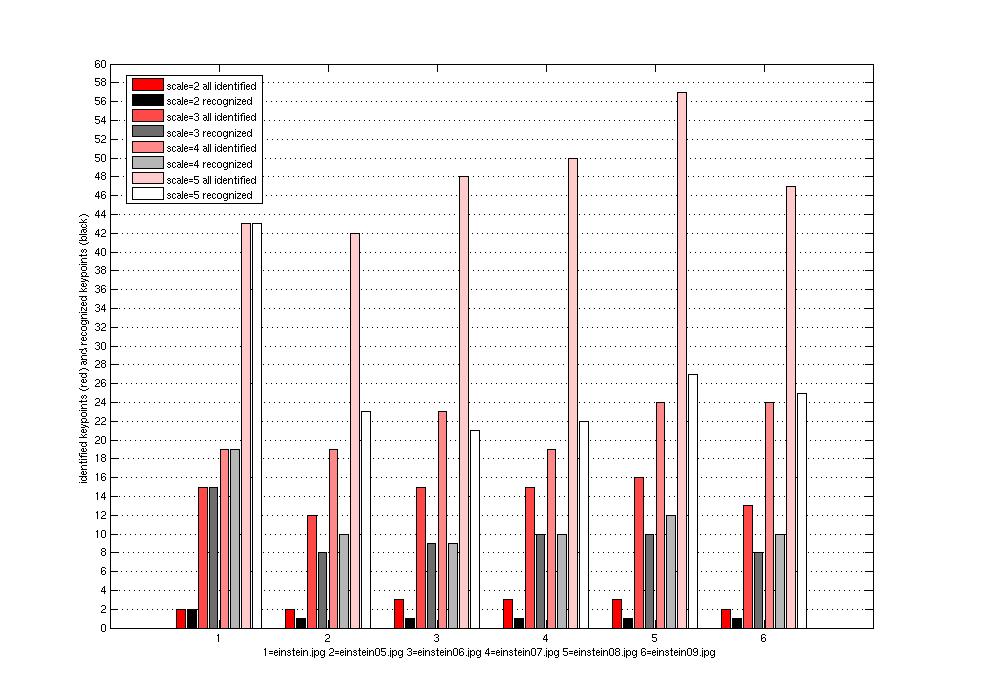
problem two
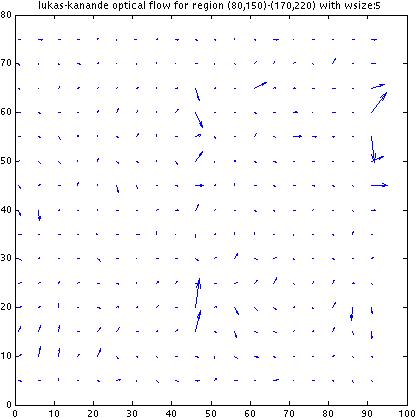
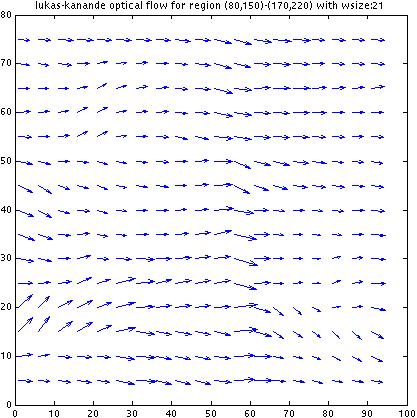
lukas-kanande optical flow tracker
source regions:
patch 0:
 |
patch 1:
 |
%% function [dx,dy] = lucaskanade(I1,I2,xl,yt,xr,yb,wsize)
%% computes the optical flow over an image region (xl->xr, yt->yb)
%% from I1 to I2 using a patch of size wsize by solving the Lucas Kanade
%% BCCE (brightness constant constraint equation)
function [lkdx,lkdy] = lucaskanade(I1,I2,xl,yt,xr,yb,wsize)
function W = getWindow(image,x,y)
%% returns window of image centered at (x,y) of size
%% (wsize)x(wsize)
half = floor(wsize/2);
W = image([y-half:y+half],[x-half:x+half]);
end;
function [bcce_dx,bcce_dy] = BCCE(x,y)
patch_dx = getWindow(i1dx,x,y);
patch_dy = getWindow(i1dy,x,y);
patch_dt = getWindow(dI,x,y);
ix2 = sum(sum(patch_dx.^2));
iy2 = sum(sum(patch_dy.^2));
ixiy = sum(sum(patch_dx.*patch_dy));
A = [ix2 ixiy; ixiy iy2];
ixit = sum(sum(patch_dx.*patch_dt));
iyit = sum(sum(patch_dy.*patch_dt));
b = -1 * [ixit; iyit];
u = pinv(A)*b; % A\b;
bcce_dx = u(1); bcce_dy = u(2);
end;
i1 = I1;
[i1dx i1dy] = gradient(i1);
% approximate the temporal gradient by a blurred difference
% between the two images
dI = blurGauss(I2,2.0)-blurGauss(I1,2.0);
lkdx = []; lkdy = [];
for xi=xl:xr,
for yi=yt:yb,
[dix,diy]= BCCE(xi,yi);
lkdx(yi-yt+1,xi-xl+1)= dix; lkdy(yi-yt+1,xi-xl+1)= diy;
end;
end;
%% kill nans
lkdx(isnan(lkdx)) = 0;
lkdy(isnan(lkdy)) = 0;
end
results:
parts b and c)
Although from visual inspection from the images it seems that
the optical flow should be the same over the whole region (the
two images are basically the result of a very slight camera
displacement to the righttos) looking at the results we see
that the conclusions that our lukas-kanande algorithm draws
are quite different.
For small window sizes, w, the algorithm is very sensitive
to local variations of brightness within the image texture,
and gets thrown off by this. In these situations, while
most of the gradients do indicate a general trend in the proper direction, many
display evidence of upwards or downwards displacmeent.
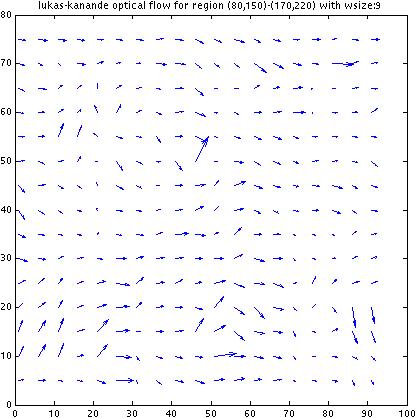
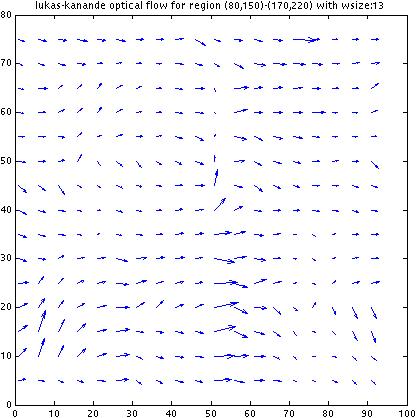
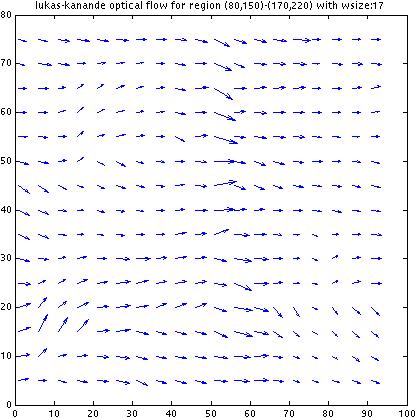
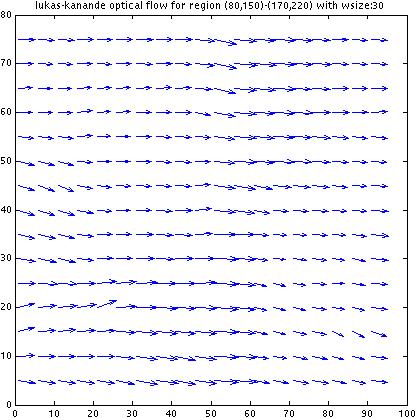
As we increase w, the optical flow vectors start to
stabilize and agree to the "correct solution". which is
fine for this particular image since the optical flow for
the whole image is the same. However, since this algorithm
computes flow within a window as if the flow at every location
within the whole patch is the same, increasing w will be
deterimental for an image where there are actual local variations
of flow. I am not sure how to get around this; that is,
how to compute flow fields for highly location-sensitive
optical flows against richly textured backgrounds.