Compositions of Cubic and Quartic Surfaces

Evdokia Nikolova, Laura Serban

enikolov@fas.harvard.edu serban@fas.harvard.edu

Computer Science 275
Harvard University
January 13, 2002


Introduction

In this project we extend the ray-tracer implemented for Computer Science 275, Assignment 6, to allow for high quality rendering of complex surfaces. Objects like ellipsoids, paraboloids, hyperboloids, cylinders, tori etc. can be described by implicit equations of degree two, three, or four. In order to render such objects, one needs to find accuate solutions to general equations of degree at most four. We explored and compared both analytical and numerical approaches to solving these equations.

Implementation

We add a new class called QUARTICS to the collection of classes that the rendered handles. This class contains functionality to render any surface that can be represented by a canonical equation of degree at most four.

We can specific any quartic surface centered at the origin of the world coordinate system by the 35 coefficients of the quadratic equation that describes it.

a0 x4 + a1 x3 y + a2 x3 z + a3 x 3 + a4 x2 y2 +
a5 x2 y z + a6 x2 y + a7 x2 z2 + a8 x2 z + a9 x2 +
a10 x y3 + a11 x y2 z + a12 x y2 + a13 x y z 2 + a14 x y z +
a15 x y + a16 x z3 + a17 x z2 + a18 x z + a19 x +
a20 y4 + a21 y3 z + a22 y3 + a23 y2 z2 + a24 y2 z +
a25 y2 + a26 y z3 + a27 y z2 + a28 y z + a29 y +
a30 z4 + a31 z3 + a32 z2 + a33 z + a34 = 0

To render the object described by the general quartic above we must perform four operations:
1. Apply the initial viewpost transformation to the quartic surface
2. Parametrize the ray and generate the equation defining the intersions points of the current ray traced and the quartic surface
3. Solve the resulting quartic equation to find its smallest positive root
4. Set the intersection point closest to the eye and compute the normal to the surface at that point of intersection

We apply the viewport transformation as follows. We decompose the modelview matrix in the corresponding rotation and translation matrices, M = RT, and we apply each transformation on the equation of the quartic surface separately. First, we apply the rotation transformation. If R transforms the basis vectors (1, 0, 0), (0, 1, 0) and (0, 0, 1) to (a1, b1, c1), (a2, b2, c2) and (a3, b3, c3), then the coefficients of the transformed equation are obtained by substituting a1x+b1y+c1z for x, a2x+b2y+c2z for y, and a3x+b3y+c3z for z into the original equation. The translation transformation is reflected in the coefficients of the quartic in a similar manner. More precisely, if r1, r2, and r3 represent the translation of the camera along the x, y and z directions, respectively, the coefficients of the translated quartic are obtained by substituting x-r1 for x, y-r2 for y and z-r3 for z in the equation of the rotated object. The tedious computation of the coefficients of the transformed equation was carried on in Mathematica and hard coded in our program.


Solving the cubics and quartics

The most challenging part of our project was the solution of higher order equations that the surfaces reduced to. We started off with the idea of implementing the well-known analytic solutions for cubics and quartics. We based our implementation on the methods presented in [2], all the more that the latter were specifically targeted to graphics.

Analytical solution to the Cubic

For the solution to a cubic of the form y3 + py2 + qy + r = 0 we set
     u = q - p2/3
     v = r - pq/3 + 2p2/27

We then set the discriminant
     j = 4(u/3)3 - v2

If j ³ 0 , we have one root. Set w = j1/2 . The root is then

     y = (((w-v)/2)1/3 + (u/3)(2/(w-v))1/3 - p/3

If j < 0 , there are three roots, given by

     y1 = 2scos(k) - p/3
     y2 = s(-cos(k) + 3(1/2)sin(k)) - p/3
     y3= s(-cos(k) - 3(1/2)sin(k)) - p/3

where
     s = (-u/3)(1/2)
     t = -v/(2s3)
     k = arccos(t)/3


Analytical solution to the Quartic

We implemented the quartic solutions of Neumark. For a quartic of the form
x4 + ax3 + bx2 + cx + d = 0 , Neumark's subsidiary cubic is


     y3 - 2by2 + (ac + b2 - 4d)y + (a2d - abc + c2) = 0

After solving this cubic as above, we use one of its roots y to form subsidiary quadratic equations whose roots would give the roots to the quartic. The two quadratics are
x2 + gx + G = 0
x2 + hx + H = 0
where
     G = (a + (a2 - 4y)(1/2))/2
     g = (a - (a2 - 4y)(1/2))/2

     H = (b-y)/2 + (a(b-y) - 2c)/(2(a2 - 4y)1/2)
     h = (b-y)/2 - (a(b-y) - 2c)/(2(a2 - 4y)1/2)

There are a number of twists to the implementation, all presented in [2] that supposedly avoid loss of precision and make the solutions to both the cubic and the quartic more stable. However, in the process of testing we realized that none of these analytic methods is trustworthy. Perhaps in 90% of the equations we got root errors of the order of the coefficients of the equations, in other words, the roots that the above algorithms output were completely off.

Switching from analytic to numerical methods

With this, we saw that the only alternative left was a numerical approach. We devised a solution to both the cubic and quartic equations based on Newton-Raphson's method.

Numerical solution to the Cubic

To solve the cubic, we find its optima by solving the quadratic equation corresponding to its derivative. Knowing the optima and their values immediately locates the regions of the roots. For example, if there are two optima, both of which are above the x-axis, we could only have one root to the left of the first optima. Since to the left of the first optima the cubic is concave down (note its first coefficient is 1 - i.e. always positive), Newton-Raphson's method with initial guess any point to the left of the optimum would unmistakably find the root. Similarly we examined the remaining cases.

Numerical solution to the Quartic

For the quartic, we used the same approach as in the cubic above. We first find its optima by numerically solving for its third degree derivative. Then, again by examining the values of the optima, we locate the regions of the roots and set our initial guesses correspondingly, calling Newton-Raphson on them.

A more subtle point was to set the initial guess for a root between two optima appropriately since the convexity of the graph changes between the optima. We noted that setting the initial guess to the inflection point between the optima always leads to finding the root in that region. Thus, for those cases we found the second derivative roots--a linear and a quadratic equation for the case of cubics and quartics respectively.

Problems and Further Improvements

Precision is currently our biggest problem. This is why we are constrained to using equations with smaller coefficients and smaller roots--to enforce that, we try to place our objects relatively close to each other and the camera at most 100-200 away.

One possibility for efficiently finding solutions to any degree polynomial equation would be to integrate ready solvers from reliable software such as Mathematica or Matlab.

Picture Gallery

Bugs Masterpieces

References

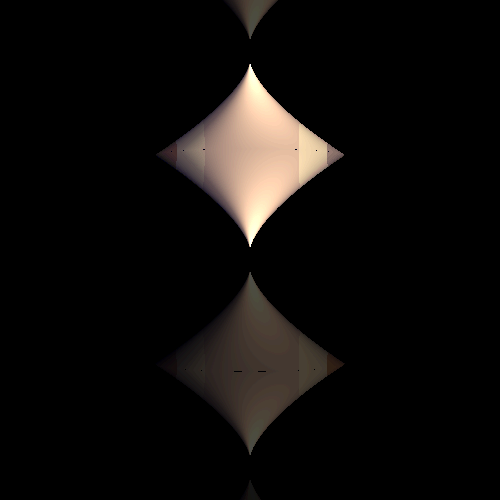
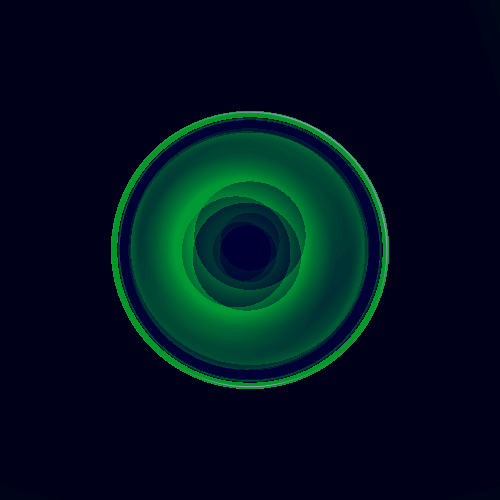
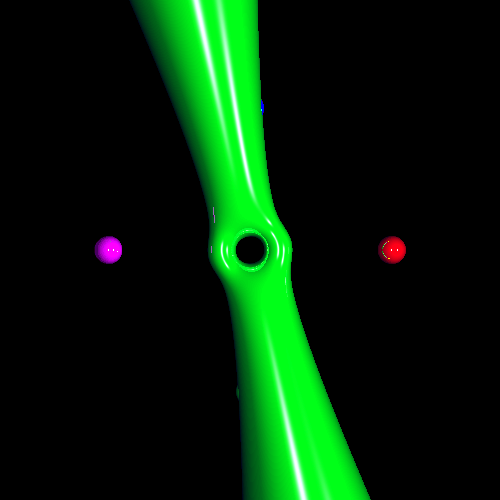
[1] D. Saupe, and Matthias Ruhl. Animation of Algebraic Surfaces.
[2] D. Herbison-Evans. Solving Quartics and Cubics for Graphics.
[3] Mathematica's Quartic Surface Equations