
That's why we introduce an origin on the line, defined by a new parameter z, and consider only the first intersection before and behind the origin.
For a given theta, the changes of visibility occur along the tangents limited by the objects.
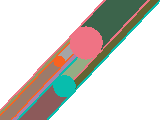
Here we show a change in the value of theta. Instead of moving the lines, we leave them vertical and turn the objects around.
Then we draw this in the dual space, and this translation and rotation gives us a cylindrical shape for each object.
Animation (780 Ko)
A line with an origin in the scene and in the dual space
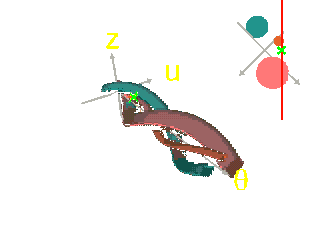
If we project onto the horizontal plane, we obtain the same curves as for the dual arrangement.
The vertices are now vertical lines between the shape of two objects.
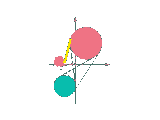

And the edges are still portions of the curves of tangency between two vertices.
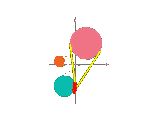

The set of lines with origin sharing the same visibility is now a volume wih vertical walls.


Now we group for a given line all origins that share the same visibility in maximal free segments.
When theta is constant, the visibility partitionning becomes a graph.
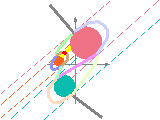
We won't represent anymore the ending faces because they are not very interesting and they are infinite.
let's draw the graph for each theta in the dual space. Note that the section is always the graph shown upper right.
Animation (1.1 Mo)
Faces that were volumes became surfaces.
This is the so called visibility complex.

Let's look inside. We can see a face, delimited by two chains of vertices and edges.
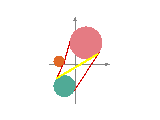

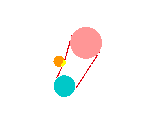

Here is an example of a segment within a face.
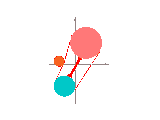
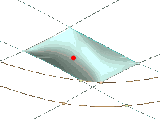
Next: Construction