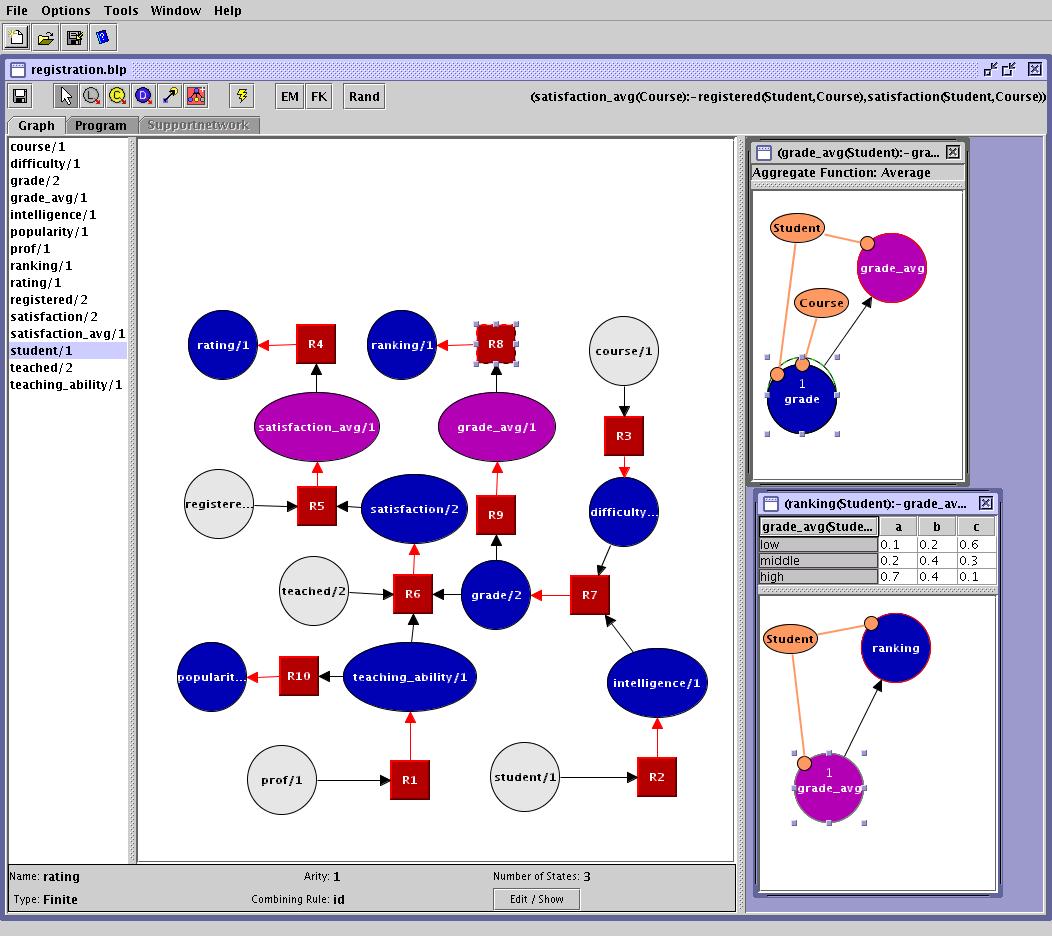
An alternative to combining rules are aggregate functions. As an example, consider the university domain due to Getoor et al., which you will find in the blp_files directory.
The university domain contains professors, students, courses, and course registrations. Objects in this domain have several descriptive attributes such as intelligence/1 and rank/1 of a student/1. A student will typically be registered in several courses; the student's rank depends on the grades she receives in all of them. So, we have to specify a probabilistic dependence of the student's rank on a multiset of course grades of size 1, 2, and so on.
In this situation, the notion of aggregation is more appropriate than that of a combining rule. Using combining rules, the Bayesian clauses would describe the dependence for a single course only. All information of how the rank probabilistically depends on the multiset of course grades would be 'hidden' in the combining rule. In contrast, when using an aggregate function, the dependence is interpreted as a probabilistic dependence of rank on some deterministically computed aggregate property of the multiset of course grades. The probabilistic dependence is moved out of the combining rule.
To model this, we introduce aggregate predicates. They represent deterministic random variables, i.e., the state of an aggregate atom is a function of the joint state of its parents. In registration.blp, avgGrade/1 is an aggregate predicate, denoted as a magenta node. As combining rule, the average of the parents' states is deterministically computed. In turn, the student's rank/1 probabilistically depends on her averaged rank.Querying P(ranking(c1)) yields
The use of aggregate functions is inspired by probabilistic relational models.