6.001 Recitation #9 – March
7, 2003
RI: Konrad Tollmar
• Tagged data
1. Self-refences structures
What is the printed form? Write an expression that generate this list.
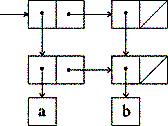
((a b) (b))
A.
‘((a b) (b))
B.
(list (list ‘a ‘b) (list ‘b))
C.
(let ((z (list ‘a ‘b))) (list z (list ‘b)))
D.
(let ((z (list ‘a ‘b))) (list z (cdr z)))
2. Tagged Data
(define (make-complex-from-rect rl im)
(list
‘rect rl im))
(define (make-complex-from-polar mg an)
(list
‘polar mg an))
(define (tag obj) (car obj))
(define (contents obj) (cdr obj))
(define (real sz)
(cond ((eq?
(tag z) ‘rect) (car (contents z)))
((eq?
(tag z) ‘polar) (* (car (contents z))
;mag
(cos (cadr
(contents z))))) ;angle
(else
(error “unknown form of object”))))
(define
(attach-tag type-tag contents)
(cons type-tag contents))
(define
(type-tag datum)
(if (pair? datum)
(car datum)
(error "Bad tagged datum --
TYPE-TAG" datum)))
(define
(contents datum)
(if (pair? datum)
(cdr datum)
(error "Bad tagged datum --
CONTENTS" datum)))
(define
(rectangular? z)
(eq? (type-tag z) 'rectangular))
(define
(polar? z)
(eq? (type-tag z) 'polar))
;;
(define
(real-part-rectangular z) (car z))
(define
(imag-part-rectangular z) (cdr z))
(define
(magnitude-rectangular z)
(sqrt (+ (square (real-part-rectangular z))
(square (imag-part-rectangular
z)))))
(define
(angle-rectangular z)
(atan (imag-part-rectangular z)
(real-part-rectangular z)))
(define
(make-from-real-imag-rectangular x y)
(attach-tag 'rectangular (cons x y)))
(define
(make-from-mag-ang-rectangular r a)
(attach-tag 'rectangular
(cons (* r (cos a)) (* r (sin a)))))
;;
(define
(real-part z)
(cond ((rectangular? z)
(real-part-rectangular (contents z)))
((polar? z)
(real-part-polar (contents z)))
(else (error "Unknown type --
REAL-PART" z))))
;;
3. Swedish (dag / månad / år) and
American ( month / day / year ) Date formats
• Data-directed programming:
functions that decide what to do based on the arguments
example:
day:
american|swedish -> number
• Defensive programming:
functions that fail gracefully if given bad arguments
Swedish dates are formatted as: (year / months / day)
American dates (month / day / year).
The idea behind data directed programming is that the data you are working with will tell you how to process it. Using attach-tag, type-tag and contents give information how to deal with this kind of information. Lets use tagged data to identify Swedish and American date values. First define a procedure that attach a tag and two access procedures that return the tag and the contents.
Attaches type-tag to contents for use with data directed programming
(attach-tag type-tag contents)
Returns the tag associated with a tagged piece of data.
(contents datum)
Returns the contents or actual data associated with a tagged
piece of data.
(attach-tag
type-tag contents)
(define birthday (make-swedish-datum 1969 3 8))
(define today (make-american-datum 3 7 2003))
(define (make-swedish-datum y m d)
(make-from-swedish-datum y m d))
(define (make-from-swedish-datum y m d)
(attach-tag 'swedish (list y m d)))
Next, lets build a procedure day (and month) that can read days and months independent of formats:
(day today) à 2
(month today)
à 10
(day
birthday) à 15
(month
birthday) à 10
1/ define a tagg check
(define (swedish? z) (eq? (type-tag z) ’swedish))
2/ define an access procedure
(define (swedish-day z) (car z))
3/ use this in a switch
(define (day z)
(cond
((swedish?
z)(swedish-day (contents z)))
((american?
z)(american-day (contents z)))
(error
"unknowed type" z)))
4. Generic operations
;; assume
(define (install-rectangular-package)
;; internal
procedures
(define
(real-part z) (car z))
(define
(imag-part z) (cdr z))
(define
(make-from-real-imag x y) (cons x y))
(define
(magnitude z)
(sqrt (+
(square (real-part z))
(square (imag-part z)))))
(define
(angle z)
(atan
(imag-part z) (real-part z)))
(define
(make-from-mag-ang r a)
(cons (*
r (cos a)) (* r (sin a))))
;;
interface to the rest of the system
(define
(tag x) (attach-tag 'rectangular x))
(put
'real-part '(rectangular) real-part)
(put
'imag-part '(rectangular) imag-part)
(put
'magnitude '(rectangular) magnitude)
(put 'angle
'(rectangular) angle)
(put
'make-from-real-imag 'rectangular
(lambda
(x y) (tag (make-from-real-imag x y))))
(put
'make-from-mag-ang 'rectangular
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
;;
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if
proc
(apply proc (map contents args))
(error
"No method for these types -- APPLY-GENERIC"
(list op type-tags))))))
;; Generic selectors
(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))