6.001 Recitation #10 – March
12, 2003
RI: Konrad Tollmar
• Data mutation
Until now we have not been able to change a variable once it has been defined. We have been programming using the functional programming paradigm, if we call a function with the same arguments we get the same result every time. Once we are allowed to change variables, this is no longer the case, procedures can now have properties that change from call to call. These properties are called state. When a variable changes we say that the state of the environment it was in has changed.
special form: set! variable [expression]
If expression is
specified, evaluates expression and stores the resulting value in the
location to which variable is bound. If expression is
omitted, variable is altered to be unassigned; a subsequent
reference to such a variable is an error. In either case, the value
of the set!
expression is unspecified.
Variable must be bound either in some region
enclosing the set!
expression, or at the top level. However, variable is permitted to
be unassigned when the set!
form is entered.
procedure: set-car! pair object
Stores object in the car
field of pair. The value returned by set-car! is unspecified.
procedure: set-cdr! pair object
Stores object in the cdr
field of pair. The value returned by set-cdr! is unspecified.
1. Evaluate these
expressions:
(define x 10)
Value:
"x --> 10"
(set! x 6) Value: 10
(+ x 3) Value: 9
x Value: 6
(set! x (+ x 3))
Value: 6
x Value: 9
(define y (cons 1 (cons 2 nil))) Value:
"y --> (1 2)"
(define z '(a b))
Value:
"z --> (a b)"
(cons y z) Value: ((1 2) a
b)
(append y z)
Value:
(1 2 a b)
(set-car! y 6)
Value:
#[unspecified]
y Value:
(6 2)
(set-cdr! y nil)
Value:
#[unspecified]
y Value:
(6)
(set-cdr! y z)
Value:
#[unspecified]
y Value:
(6 a b)
(set-car! z 12)
Value:
#[unspecified]
y Value:
(6 12 b)
(eq? (cons 'a nil) (cons 'a nil)) Value:
#f
(equal? (cons 'a nil) (cons 'a nil)) Value:
#t
(define w (list 'a 'b 'c)) Value:
"w --> (a b c)"
(eq? w (cdr (cons 'b w))) Value: #t
(eq? (cdr w) (cdr w)) Value:
#t
2. Append!
Rewrite append to append! That do not make a copy of the first list and cons'd it onto the second. Use instead side effects to append two lists without creating a copy of one of them. (Hint: define first a procedure last-pair)
(define (append lst1 lst2)
(if (null?
lst1)
lst2
(cons
(car lst1) (append (cdr lst1) lst2))))
(define (append lst1 lst2)
(set-cdr!
(last-pair lst1) lst2)
lst1)
(define (last-pair lst)
(if (null?
(cdr lst))
lst
(last-pair (cdr lst))))
3. Remember values
How does this work?
(define count (list 0))
(define (counter)
(set-car!
count (+ (car count) 1))
(car
count))
(counter) ==> ?
(counter) ==> ?
(counter) ==> ?
(define
counter
(let ((count (list 0)))
(lambda ()
(set-car! count (+ (car count) 1))
(car count)
)
)
)
Write a function called seen? that takes one argument and returns #t only if that function has been called before with that argument. Assume you have the function element? that takes an object and a list, and returns #t if the object is in the list.
(seen?
1) -> #f
(seen?
‘x) -> #f
(seen?
1) -> #t
(define
(seen?
(let ((store (list 'values)))
(lambda (x)
(if (element? x (cdr store))
#t
(begin (set-cdr! store (cons x (cdr
store))) #f)))))
(define
(element? x lst)
(cond ((null? lst) false)
((equal? (car lst) x) true)
(else (element? x (cdr lst)))))
4. Write make-ring

(define
(make-ring! ring-list)
(set-cdr! (last-pair ring-list) ring-list)
ring-list)
(define
(last-pair lst)
(if (null? (cdr lst))
lst
(last-pair (cdr lst))))
(define
ring (make-ring! (list 1 2 3 4)))
(define
ring-l (rotate-left ring)
(nth
0 ring-l) ==> 2
(define
(rotate-left ring) (cdr ring) )
(define
(ring-length ring)
(define (helper n here)
(if (eq? here ring)
n
(helper (+ 1 n) (cdr here))))
(helper 1 (cdr ring)))
(define
(rotate-right ring)
(define (helper here)
(if (eq? (cdr here) ring)
here
(helper (cdr here))))
(helper
(cdr ring)))
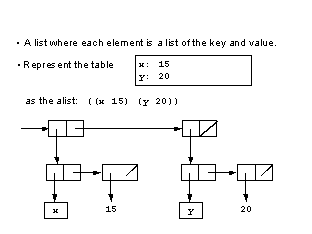
5. Traditional LISP structure: association list
(define
(find-assoc key alist)
(cond
((null?
alist) #f)
((equal?
key (caar alist)) (cadar alist))
(else
(find-assoc key (cdr alist)))))
(define a1 '((x 15) (y 20)))
(find-assoc 'y a1) ==> 20
(define (add-assoc key val alist)
(cons
(list key val) alist))
(define a2 (add-assoc 'z 10 a1))
a2 ==> ((z 10) (x 15) (y 20))
(find-assoc 'z a2) ==> 10
But - Alists are not an abstract data type
. It missing a constructor: Use quote or list to construct. So there is no abstraction barrier. Therefore, the implementation is exposed.
(define a1 ‘((x 15) (y 20)))
Lets instead use an alternative Table: a set of bindings, a pairing of a key and a value
Abstract interface to a table:
make
create
a new table
put! key value
insert
a new binding
replaces
any previous binding of that key
get key
look
up the key, return the corresponding value
This definition IS the table abstract data type
(define table1-tag .. )
(define (make-table1) .. )
(define (table1-get tbl key) .. )
(define (table1-put! tbl key val) .. )
(define table1-tag 'table1)
(define (make-table1) (cons table1-tag nil))
(define (table1-get tbl key)
(find-assoc
key (cdr tbl)))
(define (table1-put! tbl key val)
(set-cdr! tbl (add-assoc key val (cdr tbl))))