6.001 Recitation – April 16, 2003

RI: Konrad Tollmar

Quiz-2 Review:

• Data mutation

• Environment Model

• Tagged-data

• Message-passing

• OOP

Problem 1

For each of the following sets of expressions, write down what the last one will return. If it returns an error, or doesn't return at all, say so. You can assume that each set of expressions is evaluated in a fresh Scheme buffer.

(define f (lambda (y) (lambda (x) (set! x (+ x y)) x)))

(define g (f 3))

g -> (lambda (x) (set! x (+ x y)) x )

(g 4)

-> 7

(g 5)

-> 8

(define f (lambda (x) (lambda (y) (set! x (+ x y)) x)))

(define g (f 3))

(g 4)

(g 5)

(let ((n v)…) body) ==> ((l (n …) body) v … )

((l (x) body) 3 ) ==> (let ((x 3)) body)

(define g (let ((x 3)) (lambda (y) (set! x (+ x y)) x)))

->7

->12

(define g (lambda (x) (list (lambda (x) (+ x 3)) (+ x 5))))

(define h (g 1))

(cons ((car h) 7) (cdr h))

->(10 6)

(define x '(a b c))

(define y '(d e f))

(define z (append x y))

(set-car! x 'foo)

(set-car! y 'bar)

(define (append lst1 lst2)

(if (null? lst1)

lst2

(cons (car lst1) (append (cdr lst1) lst2))))

(‘foo b c)

(‘bar e f)

(a b c ‘bar e f)

Problem 2

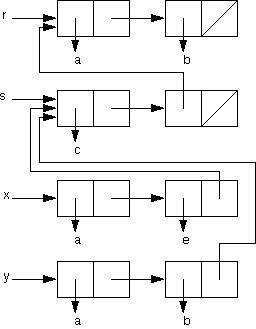
Draw a box-and-pointer diagram for r, s, x, and y that will result from evaluating the following expressions:

(define r (list 'a 'b))

(define s (list 'c 'd))

(define x (append r s))

(define y (append r s))

(set-car! (cdr x) 'e)

(set-cdr! (cdr (cdr y)) (list r))

Problem 3 (Tagged data)

You are given a list of timecard records for a given week. Some of the timecards are hourlybased:

(hourly? <obj>) > #t if <obj> is an hourly timecard

(hourlyrate <card>) > dollars per hour

(hourlyhours <card>) > list of hours worked,e.g. (8 7) or (8 8 8 8 8)

and some of the timecards are dailybased:

(daily? <obj>) > #t if <obj> is a daily timecard

(dailyrate <card>) > dollars per day

(dailydays <card>) > number of days worked this week

The following routines will help us maintain a consistent companywide typing system. These routines attach type tags to data items, and access the type and contents of the types:

(define (attachtype type contents)

(cons type contents))

(define (type datum)

(if (pair? datum)

(car datum)

(error ''Bad data object TYPE'' datum)))

(define (contents datum)

(if (pair? datum)

(cdr datum)

(error ''Bad data object CONTENTS'' datum)))

(define (istype? obj type)

(and (pair? obj)

(eq? (type obj) type)))

(define (addup proc LST)

(if (null? LST)

(+ (proc (car LST)) (addup proc (cdr LST)))))

(define (payroll cards)

(addup paycheckamount cards))

(define (paycheckamount card)

(cond ((hourly? card) (payforhourly card))

((daily? card) (payfordaily card))

(else (error ''weird timecard''))))

(define (payfordaily card)

)

(define (payforhourly card)

)

A

Your is in charge of implementing the hourly timecard abstraction. Implement hourly?, makehourly, hourlyrate and hourlyhours procedures. Show a boxandpointer diagram for a typical hourly timecard.

An example solution is:

(define (hourly? card)

  (eq? (type card) 'hourly))

(define (make-hourly rate hours)

  (attach-type 'hourly (cons rate hours)))

(define (hourly-rate card)

  (if (hourly-card? card)

      (car (contents card))

      (error "Not an hourly timecard" card)))

(define (hourly-hours card)

  (if (hourly-card? card)

      (cdr (contents card))

      (error "Not an hourly timecard" card)))

So an example box-and-pointer for (make-hourly 11.50 (list 3 4))) would be:

B

Given the payforhourly procedure was already implemented. Write a totalhoursforhourly procedure. This procedure takes an hourly timecard, and returns the total number of hours worked during the week of the timecard. Write payforhourly to use your new procedure.

An example solution is:

(define (total-hours-for-hourly card)

  (addup (lambda (x) x) (hourly-hours card)))

(define (pay-for-hourly card)

  (* (hourly-rate card)

     (total-hours-for-hourly card)))

D

Your maintains the payroll generation software (the payroll and paycheck-amount routines). The company has just added a new kind of employee, and another group has implemented the weekly timecard abstraction. ``Weekly'' employees put in a timecard at the end of any week that they happen to work, and they get paid a weekly rate, e.g. $500 per week. No one records the number of days or hours they show up, just whether or not they worked that week. How must the payroll and paycheck-amount procedures be changed to account for these weekly timecards?

An example solution is:

; This one doesn't change

(define (payroll cards)

  (addup paycheck-amount cards))

(define (paycheck-amount card)

  (cond ((hourly? card) (pay-for-hourly card))

           ((daily? card) (pay-for-daily card))

           ; This line gets added

           ((weekly? card) (pay-for-weekly card))

           (else (error "weird timecard" card))))

E

The company wants to know the total number of hours worked given a set of time cards for the week. Your are responsible for this new time accounting software. Implement totalhoursfordaily that give equivalent hours worked during the week. Define a procedure totalcompanyhours that, given a list of timecards, returns the total number of hours worked.

An example solution is:

(define (total-company-hours cards)

  (addup total-hours cards))

(define (total-hours card)

  (cond ((hourly? card) (total-hours-for-hourly card))

           ((daily? card) (total-hours-for-daily card))

           (else 0)))

Problem 4

Draw a complete environment diagram with the appropriate value or pointer to the proper environment or procedure object. Assume that the following expressions are evaluated in order.

(define (f1 x)

   (let ((a (* x x)))

      (lambda (m) (+ a x m))))

(define f2 (f1 3))

(f2 4)

(f2 5)

<1> points to the procedure object that has p: x
<2> points to the procedure object that has p: m
<3> points to the GE
<4> is 3
<5> points to E1
<6> is 9
<7> points to E2
<8> points to E2
<9> points to E2
<10> is (+ a x m)
<11> points to the GE

Problem 5 (OOPS)

1. Implement the class Machine

(define (make-machine running) (lambda (msg) (case msg ((running) (lambda (self) running)) ((start) (lambda (self) (set! running #t))) ((start) (lambda (self) (set! running #f))) (else (no-method)))))

2. Extend class Machine to a class Robot

A / Draw a class diagram that describe the class Robot.

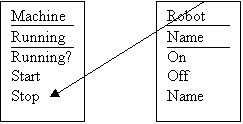
B / Implement the Robot class.

(define (make-robot name) (let ((machine (make-machine #f))) (lambda (msg) (case msg ((name) (lambda (self) name)) ((on) (lambda (self) (ask machine 'start)))((off) (lambda (self) (ask machine 'stop))) (else (get-method msg machine))))))

3. Draw an environmental diagram (model) that describes myRobot.

(define myRobot (make-robot ‘cog))