6.001
Recitation April 30, 2002
RI: Konrad Tollmar
Subroutines / Stacks
Recursion
label-name
(assign
<register-name> (reg <register-name>))
(assign
<register-name> (const <constant-value>))
(assign
<register-name> (op <operation-name>) <input1>
<input2>...)
(perform (op
<operation-name>) <input1> <input2>...)
(test (op
<operation-name>) <input1> <input2>...)
(branch (label
<label-name>))
(goto (label
<label-name>))
(assign
<register-name> (label <label-name>))
(goto
(reg <register-name>))
(save
<register-name>)
(restore
<register-name>)
1. Some more register machines
Implement for each
procedure a register machine.
(you can assume the ops: > * - = null? car cdr cons).
greater - input in
a,b; result in val
abs - input in a;
result in val
factorial - input in
n; result in prod
length - input in lst;
result in count
reverse - input in
lst; result in result
abs - input in a; result in val
(controller
(test (op >) (reg a) (const 0))
(branch (label l1))
(assign val (op *) (reg a) (const -1))
(goto (label l2))
l1
(assign val (reg a))
l2)
length - input in lst; result in count
(controller
(assign count (const 0))
loop
(test (op null?) (reg lst))
(branch (label done))
(assign count (op +) (reg count) (const 1))
(assign lst (op cdr) (reg lst))
(goto (label loop))
done)
2. Use a stack
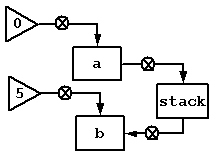
(controller
0 (assign a
(const 0))
1 (assign b
(const 5))
2 (save a)
3 (save b)
4 (restore a)
5 (restore b))
Use a stack to implement a subrutine
Save regs
Init regs
Do something
Restore regs
(save regs)
(init regs)
(assign continue (label after-subrutine))
(goto (label subrutine)
after-subrutine
(use val)
(restore regs)
subrutine
(do something)
(goto (reg continue))
Write a subroutine F(x) and use that to implement a register machine that compute F(a)/F(b).
Hint: instead of
multiply the code in the first exercise use of a subroutine and save the needed
data in a stack.
;
Contract: input in x, output in y,
; writes t
f-of-x
(assign y (const 5))
(assign t (op *) (reg x) (const 7))
(assign y (op +) (reg t) (reg y))
(assign t (op *) (reg x) (reg x))
(assign t (op *) (reg t) (const 3))
(assign y (op +) (reg t) (reg y))
(goto (reg continue))
(controller
(assign
x (reg a))
(assign
continue (label f-of-b))
(goto
(label f-of-x)) ;;
F(a)
f-of-b
(save
y)
(assign
x (reg b))
(assign
continue (label divide-em))
(goto
(label f-of-x)) ;;
F(b)
divide-em
(restore t) ; f(a)
(assign
y (op /) (reg t) (reg y))
)
3. A recursive register machine
Write the register machine corresponding to the recursive procedure to compute BN:
(define (expt b
n)
(if (= n 0)
1
(* b (expt b (- n 1)))))
(expt 4 3)
(* 4 (expt 4
2))
(* 4 (* 4 (expt
4 1)))
(* 4 (* 4 (* 4
(expt 4 0))))
(* 4 (* 4 (* 4
1)))
(* 4 (* 4 4))
(* 4 16)
64
Version 1
(assign
continue (label finish))
expt
(test ???)
(branch
(label base-case))
(save ...) ?
Version 2
- (assign continue (label finish))
- expt
- (test (op =) (reg n) (const 0))
- (branch (label base-case))
- (save continue)
- (save n)
- (assign n (op -) (reg n) (const 1))
- (assign continue (label after-loop))
- (goto (label expt))
- after-loop
- (restore n)
- (restore continue)
- (assign ans (op *) (reg b) (reg ans))
- (goto (reg continue))
- base-case
- (assign ans (const 1))
- (goto (reg continue))
- finish
L B N A C Stack
0 4 2 ? ? empty
1 4 2 ? finish empty
7 4 1 ? finish 2 finish
9 4 1 ? after-loop 2 finish
3 4 1 ? after-loop 2 finish
7 4 0 ? finish 1 after-loop 2 finish
9 4 0 ? after-loop 1 after-loop 2 finish
3 4 0 ? after-loop 1 after-loop 2 finish
16 4 0 ? a-l 1 a-l 2 finish
17 4 0 1 a-l 1 a-l 2 finish
11 4 1 1 a-l 1 a-l 2 finish
14 4 1 4 a-l 2 finish
11 4 1 4 a-l 2
finish
14 4 2 16 finish empty
18 4 2 16 finish empty
L B N A C Stack
0 4 3 ? ? empty
1 4 3 ? finish empty
7 4 3 ? finish 3 finish
9 4 2 ? after-loop 3 finish
3 4 2 ? after-loop 3 finish
7 4 2 ? after-loop 2 after-loop 3 finish
9 4 1 ? a-l 2 a-l 3 finish
3 4 1 ? a-l 2 a-l 3 finish
7 4 1 ? a-l 1 a-l 2 a-l 3 finish
9 4 0 ? a-l 1 a-l 2 a-l 3 finish
3 4 0 ? a-l 1 a-l 2 a-l 3 finish
16 4 0 ? a-l 1 a-l 2 a-l 3 finish
17 4 0 1 a-l 1 a-l 2 a-l 3 finish
11 4 0 1 a-l 1 a-l 2 a-l 3 finish
13 4 1 1 a-l 2 a-l 3 finish
14 4 1 4 a-l 2 a-l 3 finish
11 4 1 4 a-l 2 a-l 3 finish
13 4 2 4 a-l 3 finish
14 4 2 16 a-l 3 finish
11 4 2 16 a-l 3 finish
13 4 3 16 finish empty
14 4 3 64 finish empty
18 4 3 64 finish empty
4. A recursive register machine
Write the register
machine for
(define
(add-from-one-to-recursive x)
(if (= x 1)
1
(+ (add-from-one-to-recursive (- x 1))
x)))
(assign continue
(label finish))
loop
;; test and
branch for base case
;;
recursively call loop with x=x-1
;; (result
will be in ans)
;; compute
x+ans
goto (reg
continue)) ;; return
base-case
;; set answer
(goto (reg
continue)) ;; return
finish
(assign
continue (label finish))
loop
(test (op =)
(reg x) (const 0))
(branch
(label base-case))
(save
continue)
(save x)
(assign x (op
-) (reg x) (const 1))
(assign
continue (label after-loop))
(goto (label
loop))
after-loop
(restore x)
(restore
continue)
(assign ans
(op +) (reg x) (reg ans))
(goto (reg
continue))
base-case
(assign ans
(const 0))
(goto (reg
continue))
finish
5. Iterative Sum
Write the register
machine corresponding to this iterative procedure to compute S
x :
(define
(add-from-one-to x)
(define (helper x ans)
(if (= x 1)
ans
(helper (- x 1) (+ x ans))))
(helper x 1))
Unoptimized version
...
(assign ans
(const 0))
loop
(test (op =)
(reg x) (const 0))
(branch
(label done-loop))
(assign ans
(op +) (reg x) (reg ans))
(assign x (op
-) (reg x) (const 1))
(save continue)
(assign
continue (label after-call))
(goto (label
loop))
after-call
(restore
continue)
(goto (reg continue))
Optimized version
..
(assign ans
(const 0))
loop
(test (op =)
(reg x) (const 0))
(branch
(label done-loop))
(assign ans
(op +) (reg x) (reg ans))
(assign x (op
-) (reg x) (const 1))
(goto (label
loop))
done-loop