log(N) Virtual Servers

The simplest load balancing technique we discuss is log(N) VS. It balances node namespaces and does not permit arbitrary IDs. It was first introduced by Karger et al.  [25].

The log(N) VS load balancing algorithm follows from the observation that randomly chosen node IDs do not uniformly cover the identifier space. In fact, the distribution of namespaces is roughly Poisson, with the largest being $O(log(N))$ times the average.

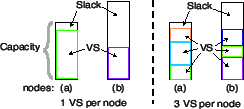
log(N) VS is predicated on the assumptions that workload and capacity are uniform. When these assumptions hold, if each node has a single VS, those few nodes at the tail become bottlenecks. By the Central Limit Theorem, the more VSs each node makes, the more normal (and balanced) the average (total) namespace of each node becomes. Because there are drawbacks to having too many VSs, this algorithm suggests that each node having $log(N)$ VS reaches a good compromise. All nodes then have average load within a constant factor. An illustration of this is shown in Figure 4. This technique is non-reactive: it makes no attempt to rebalance load after a node joins.

Figure: log(N) VS: During join, a node can divide itself into several virtual servers, which then join independently. When all nodes do this, discrepancies in the average total namespace per node diminish.

This algorithm works well for the case when its assumptions on capacities and workload distribution hold. However, increasing the number of VSs causes a few problems. First, it increases churn because when one node departs, it must take its $log(N)$ VSs with it, causing $log(N)$ times more adjustments to be made. Second, each node must hold $log(N)$ times as much routing state. Finally, because there are more VSs in the system, the number of hops per lookup (and latencies) increases. Proposals have been made to mitigate the last two problems, but they have not been evaluated [12].

Because several improvements to this basic namespace balancing concept have been proposed (see Section VII), the log(N) VS algorithm provides a baseline to suggest how this type of algorithm can be expected to perform under conditions of heterogeneity and skew in particular.