Transfer

Transfer focuses on actively unloading overloaded nodes. Instead of having underloaded nodes take on more work in isolation like Proportion, overloaded nodes following the Transfer algorithm actively seek out underloaded nodes to inquire about load transfer. Thus, nodes select arbitrary IDs at two points: when they split and when they receive transfers. This idea was first proposed by Rao et al. [35].

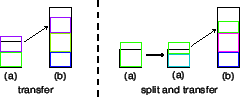
The algorithm works as shown in Figures 7 and 8. If a node is overloaded and it has only one VS, then it splits the VS into two equal parts (line 11). If a node is overloaded and if it has more than one VS (one of which may have just been created via a split), it attempts to contact an underloaded node and transfer an appropriate VS (lines 3-9). The transfer fails if all VSs would overload the potential receiver.

Figure: Transfer: Overloaded nodes attempt to transfer virtual servers to underloaded nodes. If they only have one VS and are still overloaded, they split the VS in two equal halves (and transfer one).
Figure 8: Transfer's Split and Transfer algorithm.

Transfer moves work around effectively. Nodes are never transferred work they cannot handle. However, when the system is near capacity, overloaded nodes may need to contact many others to perform a successful transfer.

Transfer has a few permutations. The scheme presented here and used in the experiments is known as ``one-to-one'' because one node contacts a single other node per unit time. The same work also proposed ``one-to-many'' and ``many-to-many'' variations and found they utilized nodes similarly. Godfrey et al. propose a more complex variation where nodes randomly choose one of a handful of well-known exchange points that periodically reallocate work [22].