Unsupervised Structure Learning: Hierarchical Composition, Suspicious Coincidence and Competitive Exclusion
Long Zhu, Chenxi Lin, Haoda Huang, Yuanhao Chen, Alan Yuille
Introduction
The goal of this paper is to learn a hierarchical compositional
model (HCM) for deformable objects. The learning is unsupervised in the sense
that we are given a training dataset of images containing the object in
cluttered backgrounds but we do not know the position or boundary of the object.
Unsupervised learning is desirable since it avoids the need for time consuming
hand labeling and prevents implicit biases. We apply the model to tasks such as
object segmentation and parsing (matching of object parts).
Learning a hierarchical compositional model is very challenging since it
requires us to learn the structure of the model (e.g. the relationships between
the variables, and the existence of hidden =
variables) in addition to the parameters of the model. The difficulties are
visually illustrated in figure~\ref{fig:taskunsupervised}: (i) the objects are
deformable so there is ambiguity in the structure. (ii) there is cluttered
background noise. (iii) parts of the object may be missing, (iv) the input is
simple oriented edge features, which is a simple and highly ambiguous
representation.
We now discuss some critical computational issues for unsupervised learning
which motivate our hierarchical approach and contrast it to other unsupervised
approaches for learning object models (e.g. \cite{Fergus03}, \cite{LZhu07}). An
abstraction of the structure learning problem is that we have a dataset of
images each of which contain approximately $M$ object features and $N$ total
features. In this paper, we are considering the case of $M=100$ and $N=5000$.
Learning an object model requires solving a complicated correspondence problem
to determine which features are object, which are background, and the spatial
relationships between the object features. There are several strategies for
addressing this correspondence problem. The first naive strategy is brute force
enumeration which involves testing all $N^M$ possibilities. This is only
practical if $M$ and $N$ are small and the appearances of the features are
sufficiently distinctive to enable many possible correspondences to be rejected.
The second strategy is to learn the model in a greedy (non-hierarchical) way by
sequentially growing subparts one by one \cite{Fergus03,LZhu07}. This is
practical in cases where brute force fails, but it still makes two assumptions:
1) sparseness assumption which requires $M$ and $N$ to be fairly small, e.g.,
$M=6$ and $N=100$ in \cite{Fergus03} and 2) small ambiguity assumption which
requires the appearances of the features to be somewhat distinctive. Neither of
these two strategies are
applicable if the features are edgelets, because $M$ and $N$ are both large and
all edgelets have the same appearance which leads to big ambiguity. (One
strategy is to use more powerful features, but we argue that this merely
postpones the complexity problem). The purpose of this paper is to develop a
more general unsupervised learning method without making strong assumptions of
sparseness and low ambiguity. In other words, we try to provide a unified
learning scheme for both generic features and object structures. Hence, we are
driven to a third strategy, named as Hierarchical Composition, that creates a
model by combining elementary structures to build a hierarchy.
Our strategy is based on a novel form of bottom-up hierarchical clustering. We
assume that the object can be expressed in terms of hierarchical compositions of
elementary structures (see the right panel of figure 1). We learn the structure
by repeatedly combining proposals for substructures to make proposals for more
complex structures. This process stops when we cannot generate any more
proposals. A huge number of proposals are examined and stored at every level to
avoid ambiguity since small substructure are not necessarily distinct enough
between object and background. However, combining proposals in this way risks a
combinatorial explosion (imagine that the number of combinations will grow
exponentially as we go up to the upper levels). We avoid this by the use
of two principles: (i) suspicious coincidences, and (ii) competitive
exclusion. Suspicious coincidences eliminates proposals which occur infrequently
in the image dataset (in less than 90 percent of the images). The competitive
exclusion principle is adapted from ecology community where it prevents two
animals from sharing the same environmental niche. In this paper, competitive
exclusion eliminates proposals which seek to explain overlapping parts of the
image.
The bottom-up clustering is followed by a top-down stage which refines and fills
in gaps in the hierarchy. These gaps can occur for two reasons. Firstly, the
competitive exclusion principle sometimes eliminates subparts of the hierarchy
because of small overlaps. Secondly, gaps may occur at low-levels of the
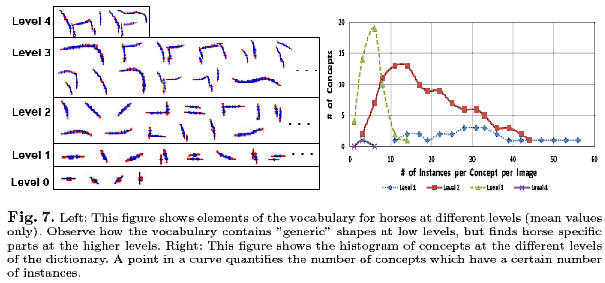
hierarchy, for example at the neck of a horse, because there are considerable
local shape variations and so suspicious coincidences are not found. The
top-down process can remove these gaps automatically by relaxing the two
principles. For example, at higher levels the system discovers more regular
relationships between the head and torso of the horse which provides context
enabling the algorithm to fill in the gaps.
In summary, hierarchical bottom-up and top-down procedure allows us to grow the
structure exponentially (the height of a hierarchy is $\log(M)$) and end up with
a nearly complete structure (the resulting representation is dense and the size
$M$ could be big). We tested our approach by using it to learn a hierarchical
compositional model for parsing and segmenting horses on Weizmann dataset
\cite{Borenstein02}. We show that the resulting model is comparable with (or
better than) alternative methods. The versatility of our approach is
demonstrated by learning models for other objects (e.g., faces, pianos,
butterflies, monitors, etc.).