

This work introduces an approach for clustering/classification which is based on the use of local, high-order structure present in the data. We define a cluster as a collection of data points that have similar local properties. Local properties are defined in terns of a relevant probability distribution over subsets of the points in the cluster. This probability distribution serves as a representation of local structure.
For some problems, this local structure might be more relevant for classification than other measures of point similarity used by popular unsupervised and semi-supervised clustering methods. Under this approach, changes in the class label are associated to changes in the local properties of the data. Using this idea, we also pursue to learn how to cluster given examples of clustered data (including from different datasets). We make these concepts formal by presenting a probability model that captures their fundamentals and show that in this setting, learning to cluster is a well defined and tractable task. Based on probabilistic inference methods, we also present an algorithm for computing the posterior probability distribution of class labels for each data point. We have tested this approach in several experiments in the domain of spatial grouping, manifold-noise separation, and functional gene classification.
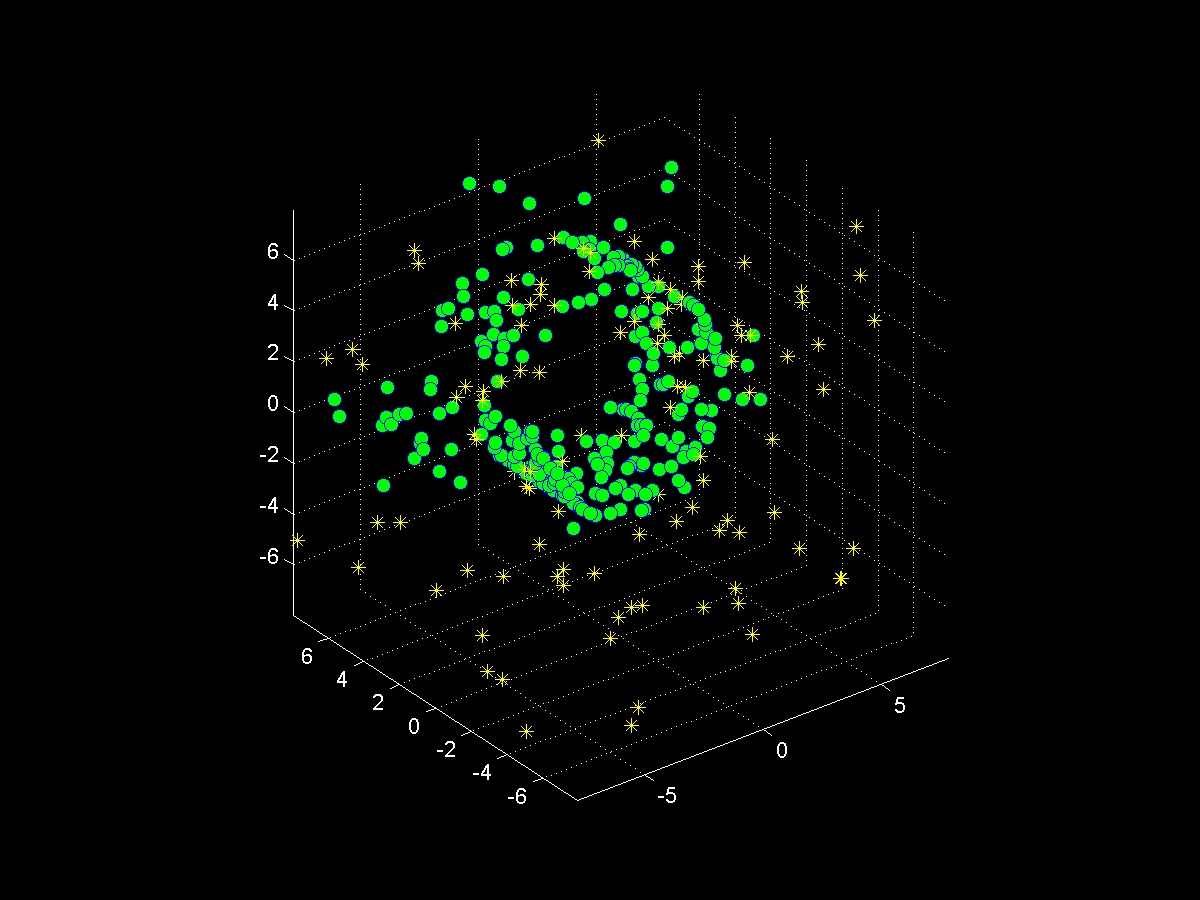
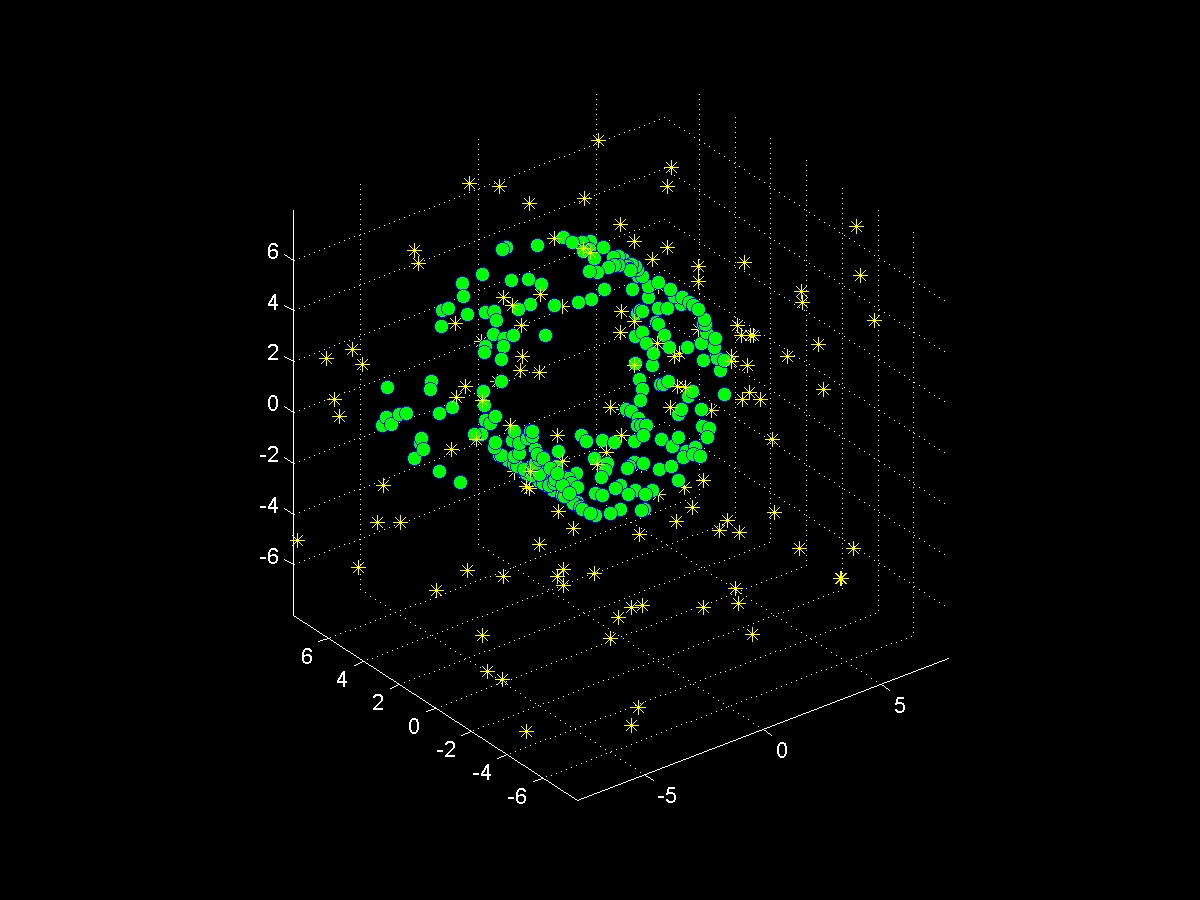
The figure below illustrates how our method separates a sampled manifold from noise points using a training data set that helps revealing the structure of the data.
 |
 |
 |
 |
| Sampled manifold+noise | Training clusters | Separated samples | Ground-truth |