
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Wednesday, February 10
The special form begin has the following form. It evaluates each one of the expressions in turn. The value of the begin expression is the value of the last expression.
(begin <expr1> <expr2> ... <exprN>)
Example:
(begin (+ 5 3) (- x 5) (* 9 9))
The special form cond has the following form. Conditional expressions are evaluated as follows. <pred1> is evaluated, and if that value is not #f, then the value of the cond clause is the value of <expr1>. If <pred1> evaluates to #f, then <pred2> is evaluated, etc.. If all of the predicates are #f, then the else expression <exprE> is evaluated and returned.

Consider the following functions similar to those presented in lecture.
(define (mul2 n m)
(define (iter count ans)
(if (= count 0)
ans
(iter (- count 1) (+ m ans))))
(iter n 0))
(define (mul3 n m)
(cond ((= n 0) 0)
((even? n)
(double (mul3 (halve n) m)))
(else
(+ m (mul3 (- n 1) m)))))
Now write a procedure mul4 that computes m*n in 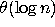 time in
time in 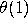 space.
space.
(define (mul4 m n)
(define (mul4-iter m count ans)
(cond ((= count 0) ans)
((even? count)
(mul4-iter (double m) (halve count) ans))
(else
(mul4-iter m (- count 1) (+ m ans)))))
(mul4-iter m n 0)
)
Consider the following two procedures.
(define (count-down x by)
(cond ((< x 0) #t)
(else (print x)
(count-down (- x by) by))))
(define (count-up x by)
(cond ((< x 0) #t)
(else (count-up (- x by) by)
(print x))))
What happens for each of
(count-down 11 3) 11 8 5 2
(count-up 11 3) 2 5 8 11
Write a function count-up-2 which performs the same way as count-up, but is an iterative process.
(define (count-up-2 x by)
(define (iter val)
(cond ((> val x) #t)
(else (print val)
(iter (+ val by)))))
(iter (modulo x by))
)
Why should we care?
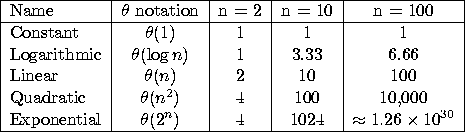
At 1 billion operations per second (current state of the art), if you
were to run an exponential time algorithm in the lab on a data set of
size n=100, you would be waiting for approximately 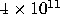 centuries for the code to finish running!
centuries for the code to finish running!
Formal Definition
Let R be some resource (e.g. space or time) used by a computation,
and suppose R is a function of the size n of a problem. The
amount of resources consumed will be 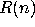 . We say
. We say 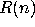 has order
of growth
has order
of growth 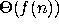 written
written 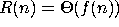 if there is some constant
if there is some constant
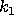 and
and 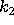 independent of n such that
independent of n such that

for sufficiently large n.
For the following functions R, find the simplest and slowest growing
function f for which 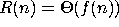 .
.
(a) 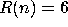
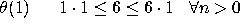
(b) 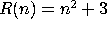
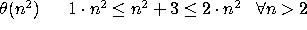
(c) 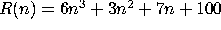
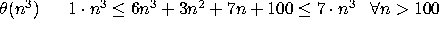
(d) 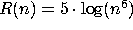
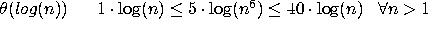
(e) 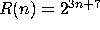
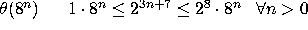
What are the Orders of Growth (space and time) for the procedures listed below?