
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Friday, February 5
Write down what Scheme will print in response to the following:

Write a procedure max of two arguments that returns the larger one.
HighlitedAnswer (define max (lambda (x y) (if (> x y) x y))) EndOfAnswer
Write a procedure sign that takes a number as its argument and returns -1 if it is negative, 1 if it is positive and 0 if the argument is zero.
HighlitedAnswer (define sign (lambda (x) (if (> x 0) 1 (if (< x 0) -1 0)))) EndOfAnswer
Consider the example below. Notice that x is used in multiple places. When do we substitute for x and when don't we?
 (define x-y*y
(lambda (x y)
(- x ((lambda (x) (* x x)) y))))
(define x-y*y
(lambda (x y)
(- x ((lambda (x) (* x x)) y))))
Use the substitution model to evaluate the following expression:
 (x-y*y 11 3)
HighlitedAnswer
(x-y*y 11 3)
HighlitedAnswer 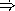 ([proc (- x ((
([proc (- x ((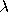 (x) (* x x)) y))] 11 3) EndOfAnswer
HighlitedAnswer
(x) (* x x)) y))] 11 3) EndOfAnswer
HighlitedAnswer 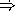 (- 11 ((
(- 11 (( (x) (* x x)) 3)) EndOfAnswer
HighlitedAnswer
(x) (* x x)) 3)) EndOfAnswer
HighlitedAnswer 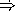 (- 11 (* 3 3)) EndOfAnswer
HighlitedAnswer
(- 11 (* 3 3)) EndOfAnswer
HighlitedAnswer  (- 11 9) EndOfAnswer
HighlitedAnswer ;Value: 2 EndOfAnswer
(- 11 9) EndOfAnswer
HighlitedAnswer ;Value: 2 EndOfAnswer
Let's examine the function below to try to better understand Scheme's scoping rules.
(define scope (lambda (x y z) (define add-to-y (lambda (x) (+ x y))) (add-to-y z)))
 (scope 1 2 3)
HighlitedAnswer ;Value: 5 EndOfAnswer
(scope 1 2 3)
HighlitedAnswer ;Value: 5 EndOfAnswer
Notice that we use lambda a lot -- in fact every time we write a function. To save us all from writing (and possibly mispelling) lamda so much, there's a short-cut.
The following two expressions are equivalent.
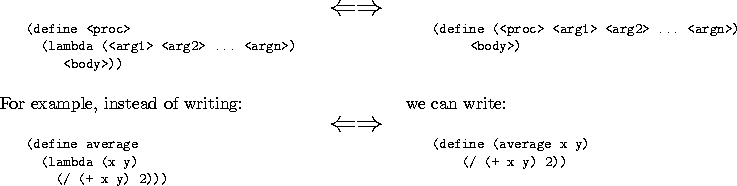
They are the same, so feel free to use either one. If the syntactic sugar is confusing, then stick with the original for now. The important thing to realize is that in both cases, the lambda expression is evaluated and then bound to the name, even if lambda isn't written anywhere.
Consider the mathematical definition of factorial:
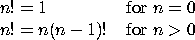
Let's write the function factorial in Scheme (using the ``Syntactic Sugar'' as described above):
(define (factorial n) HighlitedAnswer (if (= n 0) 1 (* n (factorial (- n 1)))) EndOfAnswer
)