MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999

Recitation -- Wednesday, February 10

1. More Special Forms

The special form begin has the following form. It evaluates each one of the expressions in turn. The value of the begin expression is the value of the last expression.

 
(begin <expr1> <expr2> ... <exprN>)

Example:

 
(begin (+ 5 3) (- x 5) (* 9 9))

The special form cond has the following form. Conditional expressions are evaluated as follows. <pred1> is evaluated, and if that value is not #f, then the value of the cond clause is the value of <expr1>. If <pred1> evaluates to #f, then <pred2> is evaluated, etc.. If all of the predicates are #f, then the else expression <exprE> is evaluated and returned.

2. Iterative vs Recursive Processes

Consider the following functions similar to those presented in lecture.

 
(define (mul2 n m)
  (define (iter count ans)
    (if (= count 0)
        ans
        (iter (- count 1) (+ m ans))))
  (iter n 0))

(define (mul3 n m)
  (cond ((= n 0) 0)
        ((even? n)
         (double (mul3 (halve n) m)))
        (else
         (+ m (mul3 (- n 1) m)))))

Now write a procedure mul4 that computes m*n in 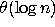time in 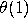space.

 
(define (mul4 m n)

)

3. More Iterative vs Recursive Processes

Consider the following two procedures.

 
(define (count-down x by)
   (cond ((< x 0) #t)
         (else (print x)
               (count-down (- x by) by))))

(define (count-up x by)
   (cond ((< x 0) #t)
         (else (count-up (- x by) by)
               (print x))))

What happens for each of

 
 (count-down 11 3)

 
 (count-up 11 3)

Write a function count-up-2 which performs the same way as count-up, but is an iterative process.

 
(define (count-up-2 x by)

)

4. Orders of Growth

Why should we care?

At 1 billion operations per second (current state of the art), if you were to run an exponential time algorithm in the lab on a data set of size n=100, you would be waiting for approximately 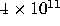centuries for the code to finish running!

Formal Definition

Let R be some resource (e.g. space or time) used by a computation, and suppose R is a function of the size n of a problem. The amount of resources consumed will be 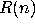. We say 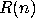has order of growth 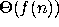written 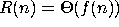if there is some constant 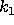and 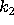independent of n such that

for sufficiently large n.

5. Order of Growth Examples

For the following functions R, find the simplest and slowest growing function f for which .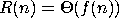

(a)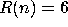

(b)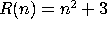

(c)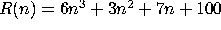

(d)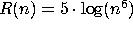

(e)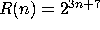

What are the Orders of Growth (space and time) for the procedures listed below?

• About this document ...