MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Wednesday, February 17
Let's look at simple operations on lists. Say I define a list as follows:
(define primes (list 2 3 5 7))
How could I make the following lists using primes?
We saw that we have the primitive function pair? to see if an object is a pair. What if we wanted to write the function list? to see if an object is a list?
What is the contract for list?
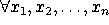(list? (list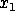 
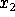
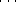
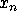)) == #t
What's another way to write it?
(list? nil) == #t (list? (cons x l)) == #t ==> (list? l)
Now, how can we write list? in scheme?
(define (list? x) HighlitedAnswer (cond ((null? x) #t) ((pair? x) (list? (cdr x))) (else #f)) EndOfAnswer)
What is the Order of Growth of pair? and list? ?
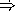
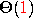and
list? is 
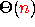HighlitedAnswer , where n is the length of the
list. EndOfAnswer
What if we wanted to reference the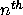 
element of a list? Write
the function list-ref that takes a list x and an integer
n and returns the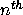 
element of the list x.
(define (list-ref x n) HighlitedAnswer (if (= n 0) (car x) (list-ref (cdr x) (- n 1))) EndOfAnswer)
Write the function length that takes a list x and returns the length of the list. Is your function iterative or recursive? Write the other one too!
Consider the procedure append that takes two lists and returns a list that results from appending the second to the first.
(define (append a b) (if (null? a) b (cons (car a) (append (cdr a) b))))
Draw the box and pointer diagrams for (append (list 1 2) (list 3 4 5)). Notice that the second list is never looked at!
Consider the procedure copy which takes a list and returns a copy of the list. How do each of the following differ?
(define (copy-ident x) x)
(define (copy-recurse x) (if (null? x) nil (cons (car x) (copy-recurse (cdr x)))))
Notice that copy-recurse is a recursive process. Let's write an iterative copy:
HighlitedAnswer Warning: the below is not copy! EndOfAnswer
(define (*copy-iter* x) HighlitedAnswer (define (aux x ans) (if (null? x) ans (aux (cdr x) (cons (car x) ans)))) (aux x nil) EndOfAnswer)
HighlitedAnswer The above is not copy. Actually, it's reverse! Now
let's define copy using reverse: EndOfAnswer
HighlitedAnswer (define (copy-iter x) (reverse (reverse x))) EndOfAnswer
Given what we learned about iterative vs. recursive processes operating on lists, write an iterative version of append.
(define (append a b) HighlitedAnswer (define (aux x ans) (if (null? x) ans (aux (cdr x) (cons (car x) ans)))) (aux (reverse a) b) EndOfAnswer )
Write the function lrange that takes a list x and two
integers a and b, and returns a list of the a'th though
the b'th elements of x. e.g. (lrange (list
0 1 2 3 4) 1 3) 
(1 2 3).
I know we're not going
to get to this in class... Try it, and the answer will be on the web.
(define (lrange x a b) HighlitedAnswer (define (n-cdrs x n) (if (= n 0) x (n-cdrs (cdr x) (- n 1)))) (define (partial-copy x n) (if (= n 0) nil (cons (car x) (partial-copy (cdr x) (- n 1))))) (partial-copy (n-cdrs x a) (+ (- b a) 1)) EndOfAnswer)