
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Friday, February 19
Let's take a look at using abstraction on common patterns.

(define make-mult (lambda (n) (lambda (x) (* n x))))
Write a function swap that takes a function f, and returns
a function, that takes two arguments, and returns f with the
variables swapped: (f x y) == ((swap f) y x) For example,
((swap -) 4 5)  1.
1.
(define swap HighlitedAnswer (lambda (f) (lambda (x y) (f y x))) EndOfAnswer )
Now try to write the function compose that takes two functions, f and g, and returns a function, that takes one argument, and composes f and g on that argument.
(define compose HighlitedAnswer (lambda (f g) (lambda (x) (f (g x)))) EndOfAnswer)
Let's trace through the evaluation of the following expression:
((compose double cube) 3)
((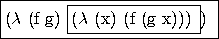 double cube) 3)
(
double cube) 3)
( 3)
(double (cube 3))
54
3)
(double (cube 3))
54
Notice that there's no magic here. We just used the same rules for evaluation that we've been using all along -- the substitution model!
Using compose, define the function ^5/2 which takes a number
x and computes 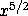 .
.
(define vspace5/2 HighlitedAnswer (compose sqrt cube) EndOfAnswer )
0.1in
We saw how to compose two procedures to produce another procedure. For example, we can define the following.
(define fourth-power (compose square square)) (define eight-power (compose square (compose square square))) ... and so on ...
Let's write a (very strange) function called repeated that takes a function f and an integer n, and composes f, n times. For example:
(define fourth-power (repeated square 2)) (define eight-power (repeated square 3)) ... and so on ...
(define (repeated proc n) HighlitedAnswer (if (= n 0) (lambda (x) x) (compose proc (repeated proc (- n 1)))) EndOfAnswer )
Let's look at a simple example:
(define fourth-power (repeated square 2)) HighlitedAnswer (repeated square 2) (compose square (repeated square 1)) (compose square (compose square (repeated square 0))) (compose square (compose square (lambda (x) x))) ... EndOfAnswer
Guess what.. Now that we've written the recursive version of repeated, let's write the iterative version.
(define (repeated proc n) HighlitedAnswer (define (iter n ans) (if (= n 0) ans (iter (- n 1) (compose f ans)))) (iter n (lambda (x) x)) EndOfAnswer )
Write a function snoc that takes two arguments a and b and returns a function, that when called with #t returns a and when called with #f returns b.

Here's an even more elegant (albeit more obscure) way of doing the same thing. Can you figure out how this is working?
(define snoc (lambda (x y) (lambda (f) (f x y)))) (define rac (lambda (p) (p (lambda (a b) a)))) (define rdc (lambda (p) (p (lambda (a b) b))))