MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999

Recitation -- Friday, February 19

1. Abstraction using Higher Order Procedures

Let's take a look at using abstraction on common patterns.

 
                                       (define make-mult 
                                         (lambda (n)  
                                           (lambda (x) 
                                             (* n x))))

3. Higher Order Procedures

Write a function swap that takes a function f, and returns a function, that takes two arguments, and returns f with the variables swapped: (f x y) == ((swap f) y x) For example, ((swap -) 4 5) 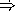1.

 
(define swap 

)

2. Composing Procedures

Now try to write the function compose that takes two functions, f and g, and returns a function, that takes one argument, and composes f and g on that argument.

 
(define compose 
)

Let's trace through the evaluation of the following expression:

 
((compose double cube) 3) 
(( double cube) 3) 
( 3)
(double (cube 3))
54

Notice that there's no magic here. We just used the same rules for evaluation that we've been using all along -- the substitution model!

Using compose, define the function ^5/2 which takes a number x and computes .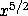

 
(define vspace5/2                         )

0.1in

5. Repeated Composition of Procedures

We saw how to compose two procedures to produce another procedure. For example, we can define the following.

 
(define fourth-power (compose square square))
(define eight-power (compose square (compose square square)))
... and so on ...

Let's write a (very strange) function called repeated that takes a function f and an integer n, and composes f, n times. For example:

 
(define fourth-power (repeated square 2))
(define eight-power (repeated square 3))
... and so on ...

 
(define (repeated proc n)

)

Let's look at a simple example:

 
(define fourth-power (repeated square 2))

6. Iterative Repeated

Guess what.. Now that we've written the recursive version of repeated, let's write the iterative version.

 
(define (repeated proc n)

)

7. More Higher-Order Procedures

Write a function snoc that takes two arguments a and b and returns a function, that when called with #t returns a and when called with #f returns b.

Here's an even more elegant (albeit more obscure) way of doing the same thing. Can you figure out how this is working?

 
(define snoc (lambda (x y) (lambda (f) (f x y))))
(define rac (lambda (p) (p (lambda (a b) a))))
(define rdc (lambda (p) (p (lambda (a b) b))))

• About this document ...