MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999

Recitation -- Wednesday, February 24

1. Abstracting Common Patterns

2. List Warm-Up

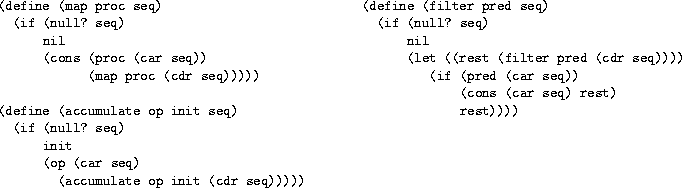
Write the following procedures using map, filter, and accumulate (no recursion!).

3. Depth of a Tree

Write a function depth that takes a tree and returns the maximum depth of the tree. Note that this is equivalent to the maximum number of parenthesis open at any given time when scheme prints the tree. For example,

 
(depth (list 1 (list (list 2) 3) (list 4))) ==> 3

 
(define (depth tree)
 
  (cond ((pair? tree)
         (max
          (+ 1 (depth (car tree)))
          (depth (cdr tree))))
        (else 0))
 )

Now write depth using map and accumulate...

 
(define (depth tree)
 
  (if (not (pair? tree))
      0
      (+ 1 (accumulate max
           0 
           (map depth tree))))
 )

4. Deep Reverse

So far, we've been working on lists, while we've ignored the elements of the list. What does the following return?
(reverse (list 1 (list 2 3) (list 4 5 6)))

Write a function deep-reverse that when called on the above tree will reverse all the elements. (deep-reverse (list 1 (list 2 3) (list 4 5 6))) ==> ((6 5 4) (3 2) 1)

 
(define (deep-reverse x)
 
  (define (aux x ans)
    (cond ((null? x) ans)
	   ((not (pair? x)) x)
           (else 
	    (aux (cdr x) (cons (deep-reverse (car x)) ans)))))
  (aux x nil)
 )

Now write deep-reverse using map...

 
(define (deep-reverse x)
 
  (if (not (pair? x)) 
      x
      (map deep-reverse (reverse x)))
 )

6. Sieve of Eratosthenes

Let's walk through the process of the sieve of Eratosthenes one more time..

 
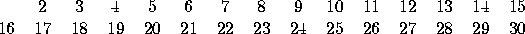
(define (sieve lst)
  (if (null? lst) 
      nil
      (cons (car lst)
            (sieve (filter (lambda (x) (not (divisible? x (car lst))))
                           (cdr lst))))))

• About this document ...