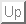(define data (list (list -1 2) (list 0 -4 3) (list 1 -1 -2))) ==> ((-1 2) (0 -4 3) (1 -1 -2))
(max-err data) ==> 5 (because 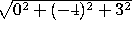 = 5 >
= 5 > 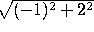 and
and 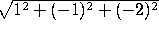 )
)


MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Friday, February 26
Write a function max-err that takes a list of lists of numbers and computes the sqrt of the maximum of the sum of the squares of the sublists. For example,
(define data (list (list -1 2) (list 0 -4 3) (list 1 -1 -2))) ==> ((-1 2) (0 -4 3) (1 -1 -2))
(max-err data) ==> 5 (because 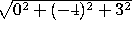 = 5 >
= 5 > 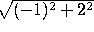 and
and 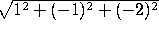 )
)
(define (max-err data) HighlitedAnswer (sqrt (accumulate max 0 (map (lambda (trial) (accumulate + 0 (map square trial))) data))) EndOfAnswer)
Say we have a list of numbers, and we want to get back a list where each number in the original list appears exactly once. For example,
(define x (list 1 2 2 3 1 5 4 3 4)) (unique x) ==> (1 2 3 5 4)
Let's write the function unique to do this. But first, write the function remove that removes all instances of an element from a list. (e.g. (remove 3 (list 1 3 2 3 4 3)) ==> (1 2 4) ).
(define (remove elt seq) HighlitedAnswer (filter (lambda (x) (not (= x elt))) seq) EndOfAnswer )
Now write unique, using remove. When writing unique, first think in English (or langunage of choice) about how you'd do this, then translate to Scheme.
(define (unique seq) HighlitedAnswer (if (null? seq) nil (cons (car seq) (unique (remove (car seq) (cdr seq))))) EndOfAnswer)
Write the function all-pairs that takes a list and returns a list of all pairs of the elements in the list. For example,
(all-pairs (list 1 2 3 4)) ==> ((1 2) (1 3) (1 4) (2 3) (2 4) (3 4))
(define (all-pairs s) HighlitedAnswer (if (null? s) nil (append (map (lambda (x) (list (car s) x)) (cdr s)) (all-pairs (cdr s)))) EndOfAnswer)
So far, we've been working on lists, while we've ignored the elements of the list. What does the following return? (reverse (list 1 (list 2 3) (list 4 5 6)))
Write a function deep-reverse that when called on the above tree will reverse all the elements. (deep-reverse (list 1 (list 2 3) (list 4 5 6))) ==> ((6 5 4) (3 2) 1)
(define (deep-reverse x) HighlitedAnswer (define (aux x ans) (cond ((null? x) ans) ((not (pair? x)) x) (else (aux (cdr x) (cons (deep-reverse (car x)) ans))))) (aux x nil) EndOfAnswer)
Now write deep-reverse using map (hint: you can use reverse)...
(define (deep-reverse x) HighlitedAnswer (if (not (pair? x)) x (map deep-reverse (reverse x))) EndOfAnswer)
Write the function flatten that takes a tree structure and returns a flat list of the leaves of the tree. For example
(fringe (list 1 (list 2) 3)) ==> (1 2 3)
(define (flatten x) HighlitedAnswer (cond ((null? x) nil) ((not (pair? x)) (list x)) (else (append (flatten (car x)) (flatten (cdr x))))) EndOfAnswer)
Now try writing flatten using map and accumulate.
(define (flatten x) HighlitedAnswer (if (not (pair? x)) (list x) (accumulate append nil (map flatten x))) EndOfAnswer)
Write the function occurrences that takes a number and a tree and counts the number of times that number appears in the tree. For example,
(define tree (list 1 2 (list (list 3 1) (list 1 2) 1))) (occurrences 1 tree) ==> 4
(define (occurrences elt tree) HighlitedAnswer (cond ((null? tree) 0) ((not (pair? tree)) (if (= elt tree) 1 0)) (else (+ (occurrences elt (car tree)) (occurrences elt (cdr tree))))) EndOfAnswer)
Now write occurrences using map and accumulate..
(define (occurrences elt tree) HighlitedAnswer (define (helper subtree) (cond ((pair? subtree) (occurrences elt subtree)) ((= subtree elt) 1) (else 0))) (accumulate + 0 (map helper tree)) EndOfAnswer)