MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999

Recitation -- Wednesday, March 31

1. Environment WHAT?

I barely remember the week before spring break. Let's start with an environment diagram warmup:

2. Counting Fibs

Recall the function fib-1 that takes an integer n and computes the n'th Fibonacci number.

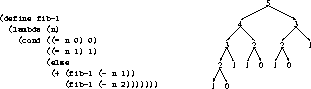
What is the Order of Growth in Time for the procedure fib-1? This is a tough one to figure out. Maybe this tree will help. Consider the number of recursive calls to fib-1 when the following is evaluated: (fib-1 5)

What if we want to see exactly how many times fib-1 is being called? Recall the function make-count-proc from last section. How can we use make-count-proc to define fib-2 that will keep a count of the number of recursive calls?

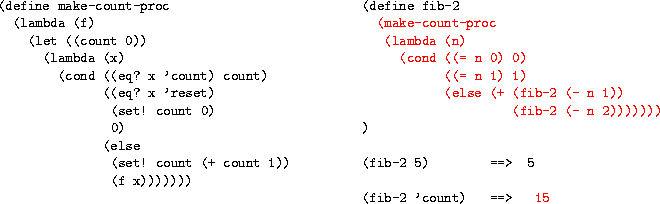
Take a look at these calls to fib-2:

 
(fib-2 'reset)          ==> 0
(fib-2 30)              ==> 832040
(fib-2 'count)          ==> 2692537

That's pretty inefficient! We're recursively calling fib-2 over and over again with the same argument and keep computing things we've already computed before. How can we fix this?

3. Memoizing

Recall that the procedure make-count-proc takes in a procedure and returns a very similar procedure (from the caller's point of view), but this new procedure keeps some local state around and does something else each time it is called.

Consider the procedure memoize that takes in a procedure of one argument and returns a procedure that keeps track of the all previously computed values. If a value passed in was passed in before, the procedure simply returns the saved value. Write the procedure memoize:

 
(define memoize 
 
  (lambda (g)
    (let ((table '()))
      (lambda (y)
        (let ((result (assoc y table)))
          (if (pair? result)
              (cadr result)
              (let ((result (g y)))
                (set! table (cons (list y result) table))
                result))))))
 )

Now define fib-3 that uses memoization and a counter.

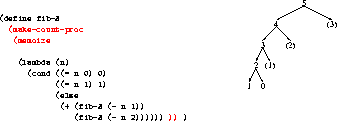
What is the Order of Growth in Time of fib-3?

 
(fib-3 'count)		==> 0
(fib-3 30)		==> 832040
(fib-3 'count)		==> 59

Challenge: Draw the Environment Diagram for the definition of fib-3 (above) and then for the expression (fib-3 3).

• About this document ...