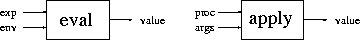
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999

Recitation -- Friday, April 9

1. Some Meta-Circular Evaluator Code

The heart of the Scheme language is an interpreter, that is, a process that evaluates legal expressions of the language. In lecture, we saw a Scheme interpreter built around the use of two basic procedures, which we will call mc-eval and mc-apply. Examples of these, without data abstractions, are given below:

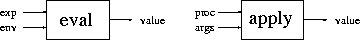
(define (mc-eval exp env) (cond ((number? exp) exp) ;base case for numbers ((symbol? exp) (lookup exp env)) ;base case for variables ((eq? (car exp) 'quote) (car (cdr exp))) ;special forms ((eq? (car exp) 'lambda) (list 'procedure (cadr exp) (caddr exp) env)) ((eq? (car exp) 'define) (eval-define (cdr exp) env)) (else (mc-apply (mc-eval (car exp) env) ;procedure application (list-of-values (cdr exp) env)))))

(define (mc-apply proc args) (cond ((atom? proc) (apply proc args)) ;primitive case ((eq? (car proc) 'procedure) ;compound procedure (mc-eval (caddr proc) ;procedure body (extend-environment (cadr proc) ;formal parameters args ;supplied arguments (cadddr proc)))) ;saved environment (else (error "Unknown procedure"))))

(define (eval-define exp env) (define-variable! (cadr exp) (mc-eval (caddr exp) env) env))

(define (define-variable! var val env) (set-car! (car env) (cons var (caar env))) (set-cdr! (car env) (cons val (cdar env))))

(define (extend-environment vars vals base-env) (cons (make-frame vars vals) base-env))

(define (make-frame vars vals) (cons vars vals))

2. An Example using the Meta-Circular Evaluator

Use the table below to trace what the Meta-Circular Evaluator does on the following three expressions. Also, use the space below the table to draw the mc-evaluator's environment.

(mc-eval '(define z (+ 1 3)) the-global-environment) (mc-eval '(define mult (lambda (x y) (* x y))) the-global-environment) (mc-eval '(mult z 3) the-global-environment)

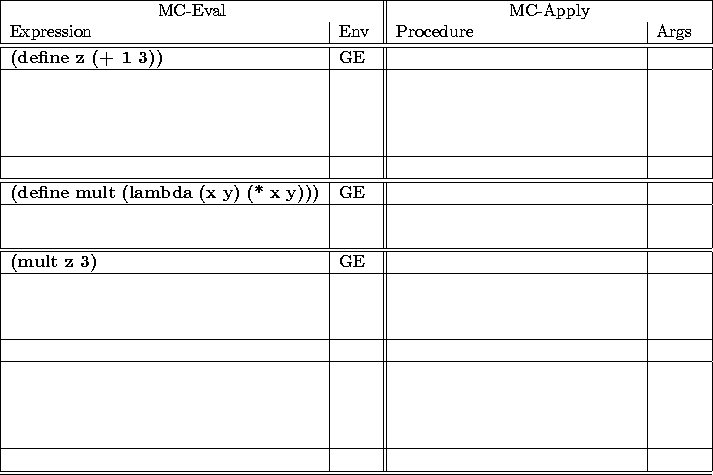
Draw the mc-evaluator's environment diagram for evaluating the above expressions.

Draw the box-and-pointer diagrams that represent the mc-evaluator's environment.

3. Adding let to the Meta-Circular Evaluator

Often we will want to add a special form to our evaluator. For example, say we want to add let. In general to add a special form, follow these steps.

1. Specify the syntax of the new special form
2. Define the data abstraction.
3. Write eval-foo where foo is your new special form either by desugaring the expression or explicitly evalating it using the rules defined by the special form.
4. Add a cond clause to mc-eval to support the new special form.

Let Form

What is the form of a let?

(let (( ) ... ( )) )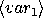

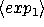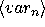
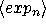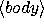Let Abstractions

You can think of let as a data-abstraction that holds three things: A list of variables, a list of expressions, and a body. We need to write the selectors for this abstraction.

(let? '(let ((a (+ 3 4)) (b 5)) (+ a b))) ==> #t (let-variables '(let ((a (+ 3 4)) (b 5)) (+ a b))) ==> (a b) (let-exps '(let ((a (+ 3 4)) (b 5)) (+ a b))) ==> ((+ 3 4) 5) (let-body '(let ((a (+ 3 4)) (b 5)) (+ a b))) ==> (+ a b)

Write the code for the following selectors:

Writing Eval-Let (Take 1)

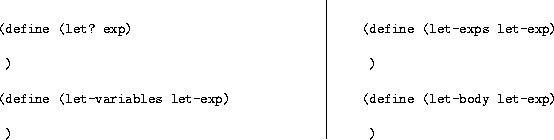
Write eval-let by desugaring:

(define (eval-let exp env) HiddenAnswer (mc-eval (cons (list 'lambda (let-variables exp) (let-body exp)) (let-values exp)) env) EndOfAnswer)

Writing Eval-Let (Take 2)

Write eval-let without desugaring:

(define (eval-let exp env) HiddenAnswer (mc-eval (let-body exp) (extend-environment (let-variables exp) (list-of-values (let-exps exp) env) env)) EndOfAnswer)

4. Brain Teasers (I have an extra page)

1. Write a scheme expression that prints itself.

(Hint: Consider how a cell reproduces. It contains its own blueprint (the DNA strand in the nucleus); reproduction involves (a) copying the blueprint, (b) implementing the blueprint. That is, it uses the blueprint twice.)

HiddenAnswer ((lambda (x) (list x (list (quote quote) x))) (quote (lambda (x) (list x (list (quote quote) x))))) EndOfAnswer

HiddenAnswer Here's another solution (my favorite):

(LET ((LET '`(LET ((LET ',LET)) ,LET))) `(LET ((LET ',LET)) ,LET)) EndOfAnswer

Write a scheme expression that goes into an infinite loop without using a define, let, or set!

HiddenAnswer ((lambda (x) (x x)) (lambda (x) (x x))) EndOfAnswer

Write a lambda expression that, when applied to a number, computes the factorial of that number without using define, let, or set! (Hint: Answer #2 first!).

HiddenAnswer (lambda (z) ((lambda (x y) (if (= y 1) 1 (* y (x x (- y 1))))) (lambda (x y) (if (= y 1) 1 (* y (x x (- y 1))))) z)) EndOfAnswer

Write the procedure list without using list or cons. (This should produce a real scheme list.)

HiddenAnswer (define (list . args) args) EndOfAnswer

Write the procedure car without using car.

HiddenAnswer (define (car first . rest) first) EndOfAnswer

Write the procedure cdr without using cdr.

HiddenAnswer (define (cdr first . rest) rest) EndOfAnswer

Write map using accumulate (no recursion).

HiddenAnswer (define (map proc x) (accumulate (lambda (x y) (cons (proc x) y)) nil x)) EndOfAnswer

Write filter using accumulate (no recursion).

HiddenAnswer (define (filter pred lst) (accumulate (lambda (x y) (if (pred x) (cons x y) y)) nil lst)) EndOfAnswer

---

• About this document ...

---

Next: About this document

---

---

Michael E. Leventon
Fri Apr 9 10:31:08 EDT 1999