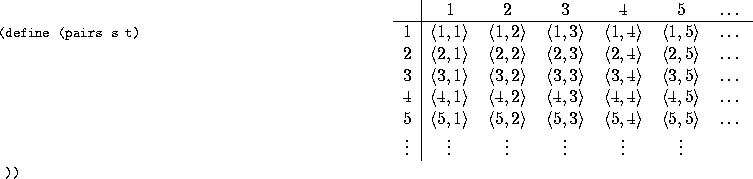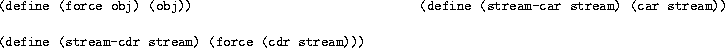
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999

Recitation -- Friday, April 16

1. Streams

In lecture yesterday, we looked at a simple implementation of streams which used two new special forms:

• (delay x) which returns a promise and is equivalent to (lambda () x)
• (cons-stream a b) which is equivalent to (cons a (delay b))

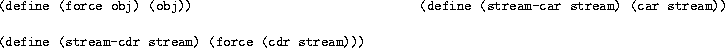
Using these basic functions, we can build infinite streams. For example:

Here's another way we can define twos using stream-map a very useful function that works like map, except on streams:

 
(define twos
  (stream-map + ones ones))

2. Warm Up

Write a procedure powers-of-2-from which takes a power of 2 ( n) and returns the stream n, n*2, (n*2)*2, ((n*2)*2)*2, ...

 
(define (powers-of-2-from n)
)

Define a stream of the whole numbers N = {0, 1, 2, 3 ...} using ones

 
(define whole  
)

3. Taylor Series

We can represent an infinite Taylor Series as a stream. The series 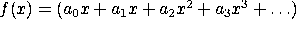can simply be represented as the stream of numbers .

Recall that (for -1 < x < 1), 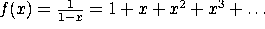. What series could we use to represent this series?

For example, recall that 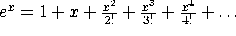. Using stream-map, fact (factorial), and whole, define the stream corresponding to this series.

 
(define enewpagex
)

4. Evaluating a Series

Now say we want to evaluate 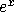for some x. Write a function eval-series that takes a series s, a value x, and the number of terms to use n, and evaluates the series.

 
(define (eval-series s x n)
)

Now we can evaluate our series:

 
(eval-series eôbeyspacesx -0.5 100)     ; value .6065306597126333

5. More Stream Tools

Write the function interleave that takes two infinite streams and interleaves them. For example

 
(define all-ints 
  (cons-stream 0 (interleave integers (stream-map - integers))))

This would be the infinite stream (0 1 -1 2 -2 3 -3 4 -4 )

 
(define (interleave s t)
)

6. Cosine Series

For example, recall that 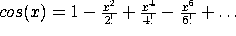. How could we create this stream using the e^x stream we already created? (What stream could we create that we could multiply with e^x?)

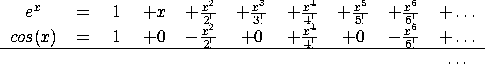
How could we define the cosine stream in this way using ones and zeros and interleave twice?

 
(define cos-x )

7. All Pairs

What about the set of all pairs of positive integers: 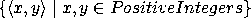? How can we capture this infinite-way infinite sequence into a stream? Let's define a procedure pairs that takes two infinite streams and returns a stream of all possible pairs of elements of the two streams.

• About this document ...