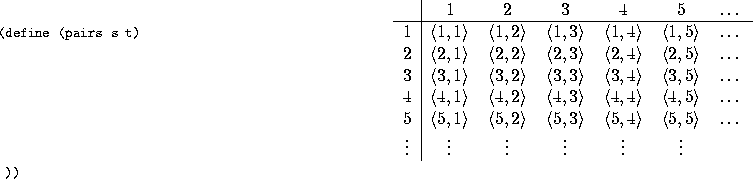
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Friday, April 16
In lecture yesterday, we looked at a simple implementation of streams which used two new special forms:
Using these basic functions, we can build infinite streams. For example:
Here's another way we can define twos using stream-map a very useful function that works like map, except on streams:
(define twos (stream-map + ones ones))
Write a procedure powers-of-2-from which takes a power of 2 ( n) and returns the stream n, n*2, (n*2)*2, ((n*2)*2)*2, ...
(define (powers-of-2-from n) HiddenAnswer (cons-stream n (powers-of-2-from (* 2 n))) EndOfAnswer)
Define a stream of the whole numbers N = {0, 1, 2, 3 ...} using ones
(define whole HiddenAnswer (cons-stream 0 (stream-map + whole ones)) EndOfAnswer)
We can represent an infinite Taylor Series as a stream. The series
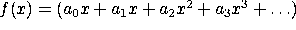can simply be represented as the stream of numbers
.
Recall that (for -1 < x < 1),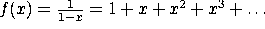 
. What series could we use to represent this series?
HiddenAnswer ones EndOfAnswer
For example, recall that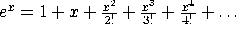 
. Using stream-map,
fact (factorial), and whole, define the stream corresponding
to this series.
(define enewpagex HiddenAnswer (stream-map (lambda (n) (/ 1 (fact n))) whole) EndOfAnswer)
Now say we want to evaluate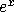 
for some x. Write a function
eval-series that takes a series s, a value x, and
the number of terms to use n, and evaluates the series.
(define (eval-series s x n) HiddenAnswer (define (iter s count ans) (if (= count n) ans (iter (stream-cdr s) (+ count 1) (+ ans (* (stream-car s) (expt x count)))))) (iter s n 0 0) EndOfAnswer)
Now we can evaluate our series:
(eval-series eôbeyspacesx -0.5 100) ; value .6065306597126333
Write the function interleave that takes two infinite streams and interleaves them. For example
(define all-ints (cons-stream 0 (interleave integers (stream-map - integers))))
This would be the infinite stream (0 1 -1 2 -2 3 -3 4 -4 
)
(define (interleave s t) HiddenAnswer (cons-stream (stream-car s) (interleave s (stream-cdr t))) EndOfAnswer)
For example, recall that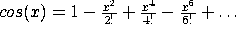 
. How could we create this
stream using the e^x stream we already created? (What stream
could we create that we could multiply with e^x?)
How could we define the cosine stream in this way using ones and zeros and interleave twice?
(define cos-x HiddenAnswer (stream-map * ecolorx (interleave (interleave ones (stream-map - ones)) zeros)) EndOfAnswer)
What about the set of all pairs of positive integers:
?
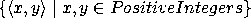How can we capture this infinite-way infinite sequence into a stream?
Let's define a procedure pairs that takes two infinite streams
and returns a stream of all possible pairs of elements of the two
streams.
