MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Friday, April 23
A register machine consists of (1) a finite set of registers, (2) a fixed set of operators, (3) a controller (set of instructions) and (4) a stack. We can represent register machines using Data Path diagrams and Controller diagrams or in a language that can be simulated in scheme.
Early in the semester, we saw some Scheme code to calculate square root using Newton's method:
(define (sqrt x) (define (good-enough? ...) ...) (define (improve guess) (average guess (/ x guess))) (define (sqrt-iter guess) (if (good-enough? guess) guess (sqrt-iter (improve guess)))) (sqrt-iter 1))
Unfortunately, Radio Shack
was out of square root chips, so we
need to implement square root ourselves. Luckily they did have an
improve chip and a good-enough? chip. Draw the data paths
and control diagram for a square root machine.
When we connect it all up, we saw that the improve chip is broken, and Radio Shack doesn't have any others. However, they did have an average chip. Redraw the data paths and control diagram as necessary to replace the improve chip. Then, convert the diagrams into a register machine.
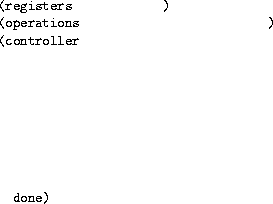
What does the following register machine compute if we assume its
input is in register x and its output is in register y.
In other words,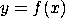 
. What's f?
HiddenAnswer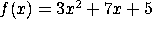 
EndOfAnswer
(registers x y t HiddenAnswer k sum EndOfAnswer) (operations * + HiddenAnswer - = EndOfAnswer) (controller HiddenAnswer (assign sum (const 0)) loop (test (op =) (reg k) (const 0)) (branch (label done)) (assign x (reg k)) EndOfAnswer (assign y (const 5)) (assign t (op *) (reg x) (const 7)) (assign y (op +) (reg t) (reg y)) (assign t (op *) (reg x) (reg x)) (assign t (op *) (reg t) (const 3)) (assign y (op +) (reg t) (reg y)) HiddenAnswer (assign k (op -) (reg k) (const 1)) (assign sum (op +) (reg sum) (reg y)) (goto (label loop)) done EndOfAnswer )
Modify the above code so that it computes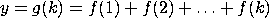 
, where k is an additional input register.
Below is the code to compute the same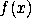 
as defined above. Given
that code, write the code to compute 
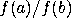, where a and
b are two input registers. You may use a continue
register and a stack. (Don't duplicate the code to compute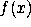 
)
(registers x y t HiddenAnswer a b continue EndOfAnswer) (operations * + HiddenAnswer / EndOfAnswer) (controller HiddenAnswer (assign x (reg a)) (assign continue (label f-of-b)) (goto (label f-of-x)) f-of-b (save y) (assign x (reg b)) (assign continue (label divide-em)) (goto (label f-of-x)) EndOfAnswer
; This is the old f(x) ; Contract: input in x, output in y, ; when done, will jump to reg continue f-of-x (assign y (const 5)) (assign t (op *) (reg x) (const 7)) (assign y (op +) (reg t) (reg y)) (assign t (op *) (reg x) (reg x)) (assign t (op *) (reg t) (const 3)) (assign y (op +) (reg t) (reg y)) (goto (reg continue))
HiddenAnswer divide-em (restore t) ; f(a) (assign y (op /) (reg t) (reg y)) EndOfAnswer )