MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001---Structure and Interpretation of Computer Programs
Spring Semester, 1999
Recitation -- Friday, May 7
Final Review Handout
Consider the two procedures below. Assume the arguments passed in are always positive integers.
(define (odd? x) (if (= x 1) #t (even? (- x 1))))
(define (even? x) (not (odd? x)))
Given the above definitions, when the expression (odd? 24) is evaluated, does that generate a recursive or iterative process? Why?
What is the order of growth of in time of the procedure even??
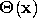EndOfAnswer
What is the order of growth of in space of the procedure odd??
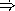
EndOfAnswer
Change one of the two functions above to make the process the opposite of what it currently is (eg. If it's a recursive process, make it iterative and if it's an iterative process, make it recursive).
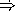
HiddenAnswer (define (even? x) (if (= x 0) #t (odd? (- x 1)))) EndOfAnswer
Consider the function below:
(define (power-of-2? n) (cond ((= n 1) #t) ((< n 1) #f) (else (power-of-2? (/ n 2)))))
Does the function power-of-2? generate a recursive or iterative process? Why?
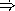
What is the order of growth of in time of the procedure power-of-2??
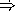
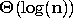EndOfAnswer
What is the order of growth of in space of the procedure power-of-2??
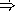
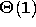EndOfAnswer
We'd like to write an evaluator for simple in-fix numerical expressions. For example, consider the trees generated by the following expressions. Careful: Notice that the operators are not quoted.
(define exp1 (list 3 + 5)) (define exp2 (list 3 * (list (list 4 + (list 6 - 2)) / 2)))
How does exp1 print when evaluated?
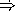
Draw the box and pointer diagram for the tree structure of exp2
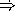
Write a function infix that evaluates these types of expressions. For example,
(infix 4) ==> 4 (infix exp1) ==> 8 (infix exp2) ==> 12
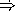
HiddenAnswer (define (infix exp) (if (not (pair? exp)) exp ((cadr exp) (infix (car exp)) (infix (caddr exp))))) EndOfAnswer
Consider a function infix->prefix that takes an infix expression
like exp1 and exp2 above, and transforms the expression
into prefix form (e.g. it swaps the order of the operator and first
operand). For example, the expression (infix->prefix (list (list
3 * 2) + 4)) will produce the same list structure as (i.e. will be
equal? with) the value of following expression:
(list +
(list * 3 2) 4).
Write the function infix->prefix.
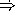
HiddenAnswer (define (infix->prefix exp) (if (not (pair? exp)) exp (list (cadr exp) (infix (car exp)) (infix (caddr exp))))) EndOfAnswer
Assume scheme has the following special form time, which takes one argument and times how long it takes to evaluate the argument. Time returns a list of two elements, the first is the amount of time it took to evaluate the expression, and the second is the value of the expression. For example,
(time (sqrt 4)) ==> (20 2) (time (sqr 5)) ==> (10 25) (time (list 1 2 3)) ==> (7 (1 2 3)) (time (/ 1 0)) ==> Error: divide by zero
Assume, for simplicity, that (sqrt x) always takes 20 time units to compute and (sqr x) always takes 10 time units to compute for all positive numbers.
Louis has a program that he wants to make run faster. He wants to see what procedures are eating up the most amount of time. He decides to write a procedure called make-timed-procedure which takes a procedure and returns a procedure that does the same thing as the original, but also keeps track of the total time spent in the procedure. For example,
(define tsqrt (make-timed-procedure sqrt)) (define tsqr (make-timed-procedure sqr))
Louis writes the following procedure:
(define make-timed-procedure-1 (let ((total-time 0)) (lambda (proc) (lambda (x) (if (eq? x 'time) total-time (let ((result (time (proc x)))) (set! total-time (+ total-time (car result))) (cadr result)))))))
After defining the following two functions, Louis trys out his code. Show the output of each of the following expressions, assuming that each call to sqrt takes 20 and each call to sqr takes 10 time units.
(define tsqrt-1 (make-timed-procedure-1 sqrt)) (define tsqr-1 (make-timed-procedure-1 sqr))
(map tsqrt-1 (map tsqr-1 '(-1 2 -3 4 -5))) ==> HiddenAnswer (1 2 3 4 5) EndOfAnswer (tsqrt-1 'time) ==> HiddenAnswer 150 EndOfAnswer (tsqr-1 'time) ==> HiddenAnswer 150 EndOfAnswer
This isn't quite the behavior we wanted. What change needs to be made to make-timed-procedure so that we get the correct behavior?
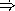
HiddenAnswer (define make-timed-procedure (lambda (proc) (let ((total-time 0)) (lambda (x) (cond ((eq? x 'time) total-time) ((eq? x 'reset) (set! total-time 0) 0) (else (let ((result (time (proc x)))) (set! total-time (+ total-time (car result))) (cadr result)))))))) EndOfAnswer
Below is the object oriented system from the March 19th Lecture Notes (just included for reference)
(define (get-method object message) (object message))
(define (no-method name) (list 'no-method name))
(define (no-method? x) (if (pair? x) (eq? (car x) 'no-method) false))
(define (method? x) (not (no-method? x)))
(define (ask object message . args) (let ((method (get-method object message))) (if (method? method) (apply method (cons object args)) (error "No method" message (cadr method)))))
Consider the following expressions:
(define (create-counter) (let ((count 0)) (lambda (message) (case message ((VALUE) (lambda (self) count)) ((INCR) (lambda (self) (set! count (+ 1 count)) count)) ((DECR) (lambda (self) (set! count (- count 1)) count))))))
(define c1 (create-counter)) (define c2 (create-counter))
Draw the environment diagram for the above three expressions.
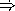
Write the expression that you would use to get the value of counter c1.
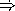
Write the expression that you would use to increment counter c1.
In this part, we are going to create an infinite stream of higher-order procedures. First, here are some simple functions that we are going to be using.
(define (compose f g) (lambda (x) (f (g x)))) (define (incr x) (+ x 1)) (define (sqr x) (* x x)
Now, Consider the function compose-fstreams that takes two streams-of-functions, fs1 and fs2, and returns another stream-of-functions where each element is the result of composing the corresponding elements of fs1 and fs2.
(define (compose-fstreams fs1 fs2) (cons-stream (compose (stream-car fs1) (stream-car fs2)) (compose-fstreams (stream-cdr fs1) (stream-cdr fs2))))
We define the following two infinite streams of functions, one that increments and one that squares.
(define fs-incr (cons-stream incr fs-incr)) (define fs-sqr (cons-stream sqr fs-sqr))
We can now define another infinite stream-of-functions fs (Hint: this is similar to how we defined integers in terms of ones).
(define fs (cons-stream incr (compose-fstreams fs-incr fs)))
What is the first element of the stream fs?
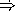
What is the second element of the stream fs?
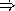
Consider the function apply-fstream and the definition of the stream s, below.
(define (apply-fstream fs x) (cons-stream ((stream-car fs) x) (apply-fstream (stream-cdr fs) x)))
(define s (apply-fstream fs 0))
What are the first 10 elements of the stream s?
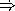
Consider the following two streams that are defined.
(define t1 (apply-fstream (compose-fstreams fs fs-sqr) 0)) (define t2 (apply-fstream (compose-fstreams fs-sqr fs) 0))
What are the first 5 elements of the stream t1?
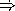
What are the first 5 elements of the stream t2?
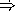
We would like to introduce a new special form to our evaluator called same?. Same? always takes three arguments, and returns #t if all three arguments are eq?. Same?, however is smart in that if the first two arguments are different, then the third argument is not evaluated. Here are some examples of using same?.
(same? 'x 'x 'x) ==> #t (same? 'x 'x 'y) ==> #f (same? 'x 'y 'y) ==> #f (same? 'x 'y (/ 1 0)) ==> #f (same? 'x 'x (/ 1 0)) ==> Divide by Zero Error
To add this special form to the evaluator, we need to define some data abstraction.
Define the function same?? that checks to see if an expression is a same? expression.
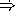
HiddenAnswer (define (same?? exp) (tagged-list? exp 'same?)) EndOfAnswer
Define the functions same?-first and same?-second that select out the first and second sub-expressions (assume someone else defined same?-third).
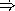
HiddenAnswer (define (same?-first exp) (cadr exp)) EndOfAnswer
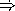
HiddenAnswer (define (same?-second exp) (caddr exp)) EndOfAnswer
Next, write the appropriate clause to add to the cond clause of eval, assuming that we have the function eval-same? that will evaluate a same? expression.
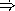
HiddenAnswer ((same?? exp) (eval-same? exp env)) EndOfAnswer
Finally, write the eval-same? function that takes a same? expression and an environment and implements the special form as described above.
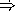
HiddenAnswer (define (eval-same? exp env) (let ((val1 (eval (same?-first exp) env)) (val2 (eval (same?-second exp) env))) (if (eq? val1 val2) (eq? val1 (eval (same?-third exp) env)) #f))) EndOfAnswer
Fill in the blanks:
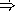
evaluation. If, instead, our language had
evaluation, then we could simply define same? as a function.
Assuming our Scheme has the alternative method of evaluation (stated in the previous paragraph), define same? as a function.
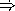
HiddenAnswer (define (same? a b c) (if (eq? a b) (eq? b c) #f)) EndOfAnswer
The special form same? from the previous example was so helpful that we decided to add it to the explicit control evaluator. Assume that in addition to the registers we've used in the past, we've also got the register TMP. Fill in the blanks in the following code that evaluates a same? expression.
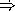
1. ev-same? 2. (assign unev (reg exp)) 3. (assign exp ((op same?-first) (reg exp))) 4. (save continue) 5. 6. (save unev) 7. (assign ) 8. (goto ) 9. eval-after-first 10. (restore unev) 11. 12. (assign tmp (reg val)) 13. (assign exp ((op same?-second) (reg unev))) 14. (save tmp) 15. 16. (save unev) 17. (assign continue eval-after-second) 18. (goto ) 19. eval-after-second 20. (restore unev) 21. 22. (restore tmp) 23. (test (op eq?) ) 24. (branch (label eval-third-arg)) 25. (assign val #f) 26. 27. (goto (reg continue)) 28. eval-third-arg 29. (assign exp ((op same?-third) (reg unev))) 30. 31. (save tmp) 32. (goto ) 33. eval-after-third 34. (restore tmp) 35. 36. (test (op eq?) ) 37. (branch (label all-same)) 38. (assign val #f) 39. (goto (reg continue)) 40. all-same 41. (assign val #t) 42. (goto (reg continue))
HiddenAnswer The special form same? is not (and cannot be) tail recursive because they're always a delayed operation to check whether the value of the third argument is eq? with the second. EndOfAnswer
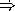
(define (foo x y) (same? (even? x) (even? y) (foo x (/ y 2))))
HiddenAnswer Recursive. There is an implicit delayed operation to check to see if the value of (even? y) is eq? with the value of (foo x (/ y 2)) EndOfAnswer
Consider the following definitions of x and y
(define x 2) (define y 3)
In the table below, list all possible final values of z after the following expressions are evaluated.
(parallel-execute (lambda () (set! x (+ y y))) (lambda () (set! y (* x y))))
(define z (list x y))
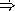
HiddenAnswer (6 18), (6 6), (9 6), (12 6) EndOfAnswer
Assume that we have one global put and get table called
*global-put-table*. Define (a simplified version of) put and
get as follows.
(put keys value) -- Places the value in the global table indexed by keys (get keys) ==> value
For example,
(put '(6001 is) 'fun) (put '(the season is) 'spring) (get '(6001 is)) ==> fun (put '(6001 is) '(almost over)) (put 'year 1999) (get 'house) ==> #f (get '(6001 is)) ==> (almost over) (get 'year) ==> 1999
Complete the following three definitions for put and get.
(define *global-put-table* HiddenAnswer '() EndOfAnswer )
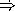
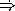
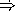
Draw the Data Paths AND Controller for a machine to compute whether the input x is odd by successively subtracting 1 from the input. You can assume that the input will be a positive integer. Assume the only primitive operations you have are subtraction, logical not, and testing equality. After your machine finishes running, the result in the answer register should be either #t or #f.
Consider the following compiled code:
1. (assign val (op make-compiled-procedure) (label entry23) (reg env)) 2. (goto (label after-lambda22)) 3. entry23 4. (assign env (op compiled-procedure-env) (reg proc)) 5. (assign env (op extend-environment) (const (f c)) (reg argl) (reg env)) 6. (save continue) 7. (save env) 8. (assign proc (op lookup-variable-value) (const c) (reg env)) 9. (assign val (op lookup-variable-value) (const f) (reg env)) 10. (assign argl (op list) (reg val)) 11. (test (op primitive-procedure?) (reg proc)) 12. (branch (label primitive-branch29)) 13. compiled-branch28 14. (assign continue (label proc-return30)) 15. (assign val (op compiled-procedure-entry) (reg proc)) 16. (goto (reg val)) 17. proc-return30 18. (assign proc (reg val)) 19. (goto (label after-call27)) 20. primitive-branch29 21. (assign proc (op apply-primitive-procedure) (reg proc) (reg argl)) 22. after-call27 23. (restore env) 24. (restore continue) 25. (assign val (op lookup-variable-value) (const f) (reg env)) 26. (test (op false?) (reg val)) 27. (branch (label false-branch25)) 28. true-branch26 29. (assign val (const 1)) 30. (goto (label after-if24)) 31. false-branch25 32. (assign val (const 2)) 33. after-if24 34. (assign argl (op list) (reg val)) 35. (assign val (op lookup-variable-value) (const a) (reg env)) 36. (assign argl (op cons) (reg val) (reg argl)) 37. (test (op primitive-procedure?) (reg proc)) 38. (branch (label primitive-branch33)) 39. compiled-branch32 40. (assign val (op compiled-procedure-entry) (reg proc)) 41. (goto (reg val)) 42. primitive-branch33 43. (assign val (op apply-primitive-procedure) (reg proc) (reg argl)) 44. (goto (reg continue)) 45. after-call31 46. after-lambda22 47. (perform (op define-variable!) (const a) (reg val) (reg env)) 48. (assign val (const ok))
Decompile the following groups of code. (Hint: Don't worry if the overall code looks a bit unusual.)
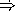
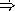
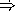
HiddenAnswer (define a (lambda (f c) ((c f) a (if f 1 2)))) EndOfAnswer