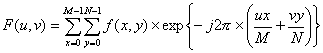 (1)
(1)Preprocessing Algorithm
To getting better fingerprint images, we need to do:
1. Histogram Equalization:
In this step, we want to adjust the contrast of the original fingerprint images (Figure 1(b)).
2. Image Enhancement [3]:
We divide the image into small processing blocks ( 32 by 32 pixels) and perform the Fourier transform according to:
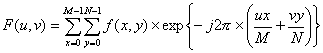 (1)
(1)
for u = 0, 1, 2, ..., 31 and v = 0, 1, 2, ..., 31.
In order to enhance a specific block by its dominant frequencies, we multiply the FFT of the block by its magnitude a set of times. To get the magnitude of the original FFT, we need to multiply the original FFT and the inverse FFT. The inverse FFT is done by:
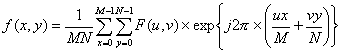 (2)
(2)
for x = 0, 1, 2, ..., 31 and y = 0, 1, 2, ..., 31, and
![]() (3)
(3)
where g(x,y) is the enhancement block and k is an experimentally determined constant, which we choose k=0.45 to calculate. While having a higher "k" improves the appearance of the ridges, filling up small holes in ridges, having too high a "k" can result in false joining of ridges. Thus a termination minutiae might become a bifurcation. Figure 1(c) presents the image after FFT enhancement.
3. Image Enlargement:
Since we need larger image to make sure we could extract the correct minutiaes from the images, we choose the "Bilinear" algorithm to achieve this goal according to the homework #2. Figure 1(c) shows the result images after bilinear enlargement.
4. Binarization [4]:
Based on Brink [4], we use the maximum correlation between the original and threshold images as the threshold values to binarize the images. If the pixel values is greater than the threshold value, we set the pixel values as 255. Otherwise, we set the pixel value as 0. Figure 1(d) depicts the binarized image.


(a) (b)

(c)

(d)
Figure 1:
(a) A original fingerprint image.
(b) The histogram image of the original image from (a).
(c) The image of the image from (b) after FFT filter and bilinear enlargement.
(d) The binary image of the image from (c).