What

We propose a system to estimate noise level from a single color image. We illustrate the utility of this noise estimation for two algorithms: edge detection and feature preserving smoothing through bilateral filtering. This work was mostly done when Ce Liu interned at Interactive Visual Media Group, Microsoft Research in the summer of 2005.

Why

Image denoising has been intenstively studied in both image processing and computer vision literature. In most denoising work the noise level is often assumed to be known as AWGN [1]. However, we found the noise from CCD camera is not additive and the noise level is really unknown, depending on the camera and setting such as ISO, shudder speed and aperture. Therefore, we are motivated to estimate noise level from a single image so that denoising algorithm can be automatic and more effective. We also find that noise level is a magic parameter in many computer vision algorithms. Knowing noise level makes these algorithms more adaptive to the input.

How

Estimating the noise level from a single image seems like an impossible task: we need to recognize whether local image variations are due to color, texture, or lighting variations from the image itself, or due to the noise. It might seem that accurate estimation of the noise level would require a very sophisticated prior model for images. However, in this work we use a very simple image model--piecewise smooth over segmented regions--to derive a bound on the image noise level. We fit the image data in each region with a smooth function and estimate the noise using the residual. Such estimates are guaranteed to be over-estimates of the true noise variance, since the regions can contain image variations that are not being modeled. However, there are usually some regions in each image for which the simple model holds, and we find that our noise bounds are usually tight. While we assume that auxiliary camera information is unknown, the algorithm proposed in this paper can easily be augmented with such information.

Unfortunately, real CCD camera noise is not simply additive; it is strongly dependent on the image intensity level. We call the noise level as a function of image intensity the noise level function, or NLF. Since it may not be possible to find image regions at all the desired levels of intensity or color needed to describe the noise level function, we use the Columbia camera response function database [2] to model the NLF using principal components and bounds on derivatives (see Figure 1). These principal components serve as a prior model to estimate the NLF over regions of missing data. We use a Bayesian MAP framework to estimate the noise level functions in RGB channels, using the bounds derived from the noise estimates over each image region.

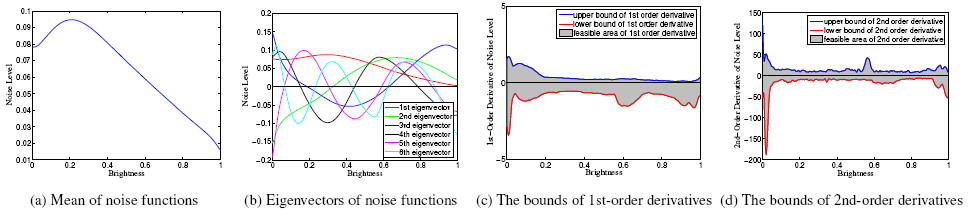
Figure 1. Camera noise function properties.

Experiments on both synthetic and real data demonstrate that the proposed algorithm can reliably infer noise levels. Some estimated NLFs are shown in Figure 2. In (a) we observe many texture regions especially at high intensity values, which implies high signal variance. The estimated curves (in red, green and blue) do not tightly follow the lower envelope of the samples at high intensities, although they deviate from the true noise function (in gray) slightly. In (b) the samples do not span the full intensity range, so our estimate is only reliable where the samples appear. This shows a limit of the prior model: the samples are assumed to be well-distributed. The estimation is reliable if the color distribution span the full range of the spectrum and there are textureless regions, as in (c). Please refer to [3] for the experiment on images taken using real CCD camera.

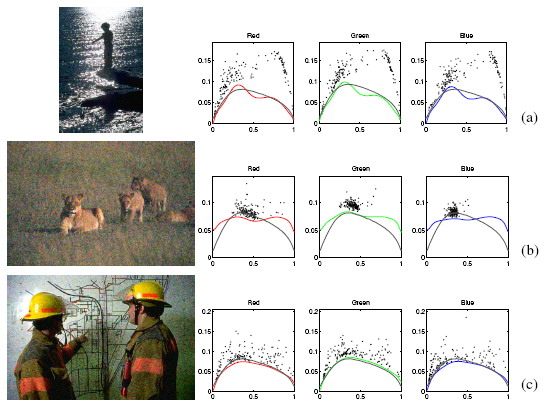
Figure 2. Synthetic noisy images and their corresponding noise estimation

Applications

Noise estimation is a very useful for many computer vision algorithms. We design noise adaptive bilateral filtering and Canny edge detector without user specified parameter for each input. The comparison with standard algorithms is shown in Figure 3. Four synthetic noise contaminated images (a) are obtained by increasing σ_s and σ_c. Noise level functions as inferred by our algorithm from each image (b). (c) Classical bilateral filtering with constant parameter setting. Note the sensitivity of the output to the input noise level. (d) Adaptive bilateral filltering exploiting inferred noise levels, leading to robust performance independent of noise level. (e) Canny edge detection using the automatic parameter settings supplied in MATLAB^TM program, which attempt to adapt to the input image. Despite adaptation, the algorithm does not adequately compensate for the changes in image noise level. (f) Canny edge detection after adapting algorithm parameters using inferred noise level functions. Algorithm performance is now substantially independent of the image noise levels.

Figure 3. Application of noise estimation

Acknowledgement

Ce Liu is supported by Microsoft Fellowship.

References:

[1] J. Portilla, V. Strela, M. J. Wainwright, and E. P. Simoncelli. Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Trans. on Image Processing, 12(11):1338--1351, Nov 2003.

[2] M. D. Grossberg and S. K. Nayar. Modeling the space of camera response functions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26(10):1272--1282, October 2004.

[3] C. Liu, W.T. Freeman, R. Szeliski and S.B. Kang. Noise estimation from a single image. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 901-908, 2006 [pdf].