Next: Il metodo d'inversione
Up: Impostazione matematica del problema
Previous: Introduzione all'algoritmo
Contents
Per semplicità si pone 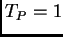 nell'equazione (2.5).
Se si calcola la trasformata di Fourier di ambo i membri, si ottiene:
nell'equazione (2.5).
Se si calcola la trasformata di Fourier di ambo i membri, si ottiene:
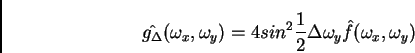 |
(2.6) |
dove
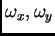 sono le frequenze associate alle variabili spaziali
sono le frequenze associate alle variabili spaziali
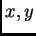 .
.
Come già osservò Beckers [1], l'equazione (2.6) evidenzia
che l'immagine chopped and nodded, così come l'immagine
chopped, non contiene informazioni sulla
trasformata di Fourier
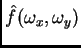 alle frequenze
alle frequenze
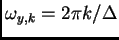 (con
(con
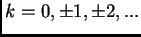 ),
anche se
),
anche se
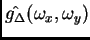 è diversa da zero in tali frequenze
a causa del noise che contamina la
è diversa da zero in tali frequenze
a causa del noise che contamina la
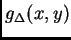 .
.
Per questo motivo la ricostruzione di
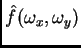 non
può essere ottenuta dividendo l'equazione (2.6) per il fattore
non
può essere ottenuta dividendo l'equazione (2.6) per il fattore
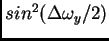 ;
in effetti calcolare l'immagine
;
in effetti calcolare l'immagine 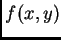 , partendo dall'acquisizione
, partendo dall'acquisizione
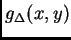 risulta un problema ``mal posto''.
risulta un problema ``mal posto''.
Per ovviare a questo inconveniente si possono utilizzare metodi di
regolarizzazione [2].
In generale questi non possono far ricorso a metodi di Fourier,
poiché 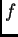 e
e 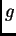 sono definite su domini diversi.
Infatti, se la regione da prendere in considerazione corrisponde all'intervallo
sono definite su domini diversi.
Infatti, se la regione da prendere in considerazione corrisponde all'intervallo
![$[0,Y]$](img72.png) nella variabile
nella variabile 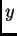 ,
,
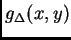 è ivi definita (per
è ivi definita (per 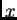 fissato) ma, come
si può dedurre dall'equazione (2.5), essa riceve contributi dai valori
di
fissato) ma, come
si può dedurre dall'equazione (2.5), essa riceve contributi dai valori
di 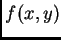 nell'intervallo
nell'intervallo
![$[-\Delta,Y+\Delta]$](img74.png) , che è molto più ampio di
, che è molto più ampio di
![$[0,Y]$](img72.png) . Un metodo che ricostruisca
. Un metodo che ricostruisca 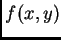 in questo intervallo porterà un
aumento del range.
Di questo fatto si deve tenere conto quando si discretizza il problema.
in questo intervallo porterà un
aumento del range.
Di questo fatto si deve tenere conto quando si discretizza il problema.
Assumiamo che il piano del detector sia suddiviso in 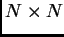 pixels ciascuno con dimensione
pixels ciascuno con dimensione
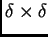 , etichettati con indice
, etichettati con indice
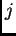 , corrispondente alla colonna (variabile
, corrispondente alla colonna (variabile 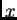 ) e con indice
) e con indice 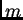 corrispondente
alla riga (variabile
corrispondente
alla riga (variabile 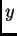 ) dell'array.
Inoltre supponiamo che la direzione del movimento di chopping sia parallela alle
colonne e che l'ampiezza di chopping
) dell'array.
Inoltre supponiamo che la direzione del movimento di chopping sia parallela alle
colonne e che l'ampiezza di chopping  sia un multiplo della distanza
di campionamento
sia un multiplo della distanza
di campionamento 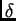 (
(
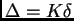 ). Spesso consideriamo la maggior parte
delle immagini delle
). Spesso consideriamo la maggior parte
delle immagini delle  con
con  tipicamente (ma non necessariamente) fra
30 e 50.
tipicamente (ma non necessariamente) fra
30 e 50.
Se 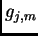 e
e 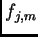 sono rispettivamente i campioni di
sono rispettivamente i campioni di 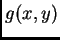 e
e 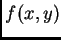 ,
per ogni indice
,
per ogni indice 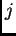 , i valori
, i valori 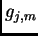 (con
(con 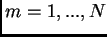 ) formano un vettore di
lunghezza
) formano un vettore di
lunghezza 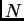 che denoteremo con
che denoteremo con
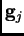 . Esso riceve contributi dagli
. Esso riceve contributi dagli 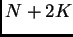 valori di
valori di 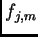 (
(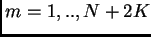 ) il quale forma un vettore
) il quale forma un vettore
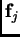 di
lunghezza
di
lunghezza 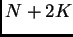 .
Le componenti di
.
Le componenti di
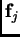 con
con 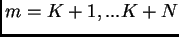 corrispondono ai punti di
campionamento nella regione di interesse, che chiameremo
regione d'osservazione.
corrispondono ai punti di
campionamento nella regione di interesse, che chiameremo
regione d'osservazione.
Con le notazioni sopra citate, l'equazione (2.5) viene modificata, in
termini discreti, nella relazione:
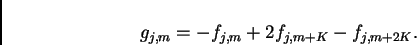 |
(2.7) |
Introduciamo ora la matrice di imaging ![$[A]$](img92.png) definita come:
definita come:
![\begin{displaymath}[A]_{m,n}=-\delta_{m,n}+2\delta_{m+K,n}-\delta_{m+2K,n} \,\,
\end{displaymath}](img93.png) |
(2.8) |
dove 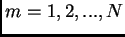 e
e
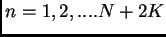 ed inoltre vale:
ed inoltre vale:
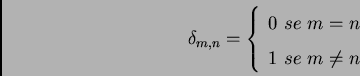 |
(2.9) |
In notazione matriciale l'equazione (2.7) diventa:
![\begin{displaymath}
\mathbf{g}_{j}=[A]\mathbf{f}_{j}. \,\,
\end{displaymath}](img97.png) |
(2.10) |
![$[A]$](img92.png) è una matrice rettangolare con
è una matrice rettangolare con 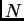 righe e
righe e 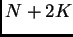 colonne. Ne segue
che il sistema lineare dell'equazione (2.10) è sottodeterminato e,
per ogni
colonne. Ne segue
che il sistema lineare dell'equazione (2.10) è sottodeterminato e,
per ogni
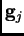 , ci sono almeno
, ci sono almeno 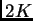 soluzioni linearmente
indipendenti.
soluzioni linearmente
indipendenti.
Dato che la matrice di imaging non dipende dall'indice 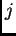 ,
il problema di ricostruzione di immagini si riduce al problema di risolvere
l'equazione (2.10) per ogni colonna dell'immagine.
,
il problema di ricostruzione di immagini si riduce al problema di risolvere
l'equazione (2.10) per ogni colonna dell'immagine.
Poiché la matrice ![$[A]$](img92.png) risulta mal condizionata, la soluzione è
numericamente instabile e di ciò occorrerà tenere conto.
Utilizzando il modello descritto dall'equazione (2.10), però, si
commettono diversi tipi di errori:
risulta mal condizionata, la soluzione è
numericamente instabile e di ciò occorrerà tenere conto.
Utilizzando il modello descritto dall'equazione (2.10), però, si
commettono diversi tipi di errori:




Next: Il metodo d'inversione
Up: Impostazione matematica del problema
Previous: Introduzione all'algoritmo
Contents
Anna Custo
2002-02-05