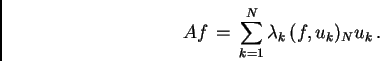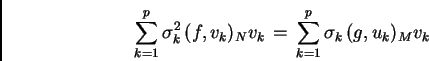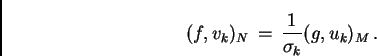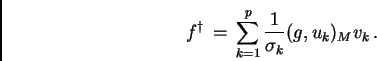Next: Codice prodotto
Up: Algoritmi matematici utilizzati
Previous: Metoto iterativo di Landweber-Fridman
Contents
Decomposizione in valori singolari di una matrice
Se si considera una matrice 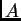 simmetrica, di dimensioni
simmetrica, di dimensioni 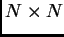 ,
con elementi reali tale che
,
con elementi reali tale che
Allora esiste una matrice diagonale 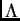 e una matrice ortogonale
e una matrice ortogonale 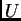 tali che
tali che
Gli elementi diagonali di 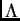 ,
,
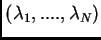 , costituiscono
gli autovalori di
, costituiscono
gli autovalori di 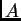 ; le colonne di
; le colonne di 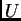 ,
,
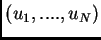 , costituiscono gli
autovettori di
, costituiscono gli
autovettori di 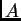 , associati ai rispettivi autovalori, essi sono soluzioni dei
problemi:
, associati ai rispettivi autovalori, essi sono soluzioni dei
problemi:
Gli autovettori sono ortonormali rispetto al prodotto scalare euclideo, ovvero:
dove 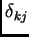 è il simbolo di Kronecker.
è il simbolo di Kronecker.
La forma diagonale di 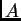 implica la seguente rappresentazione spettrale:
implica la seguente rappresentazione spettrale:
Se la matrice 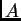 è semidefinita positiva, cioè se
è semidefinita positiva, cioè se
allora
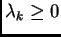 .
.
Se 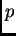 è il rango della matrice, si possono
ordinare gli autovalori in modo tale che
è il rango della matrice, si possono
ordinare gli autovalori in modo tale che
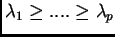 ,
,
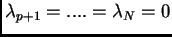 .
.
Se 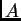 è positiva, cioè se
è positiva, cioè se
allora
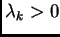 (cioè
(cioè 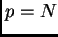 ) e si possono ordinare gli autovalori in
modo tale che
) e si possono ordinare gli autovalori in
modo tale che
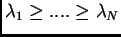 .
.
Il caso più generale, però, è quello in cui la matrice 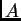 è rettangolare,
di dimensioni
è rettangolare,
di dimensioni 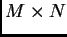 , e rango
, e rango 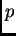 .
.
Se 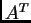 è la matrice trasposta di
è la matrice trasposta di 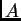 , si considerino le matrici
, si considerino le matrici 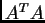 di
dimensioni
di
dimensioni 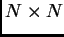 con autovettori
con autovettori 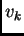 e
e 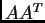 di dimensioni
di dimensioni 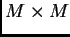 con autovettori
con autovettori 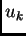 .
Si può dimostrare che tali matrici sono simmetriche e semidefinite (o definite)
positive; inoltre queste matrici hanno gli stessi autovalori (che indicheremo
con
.
Si può dimostrare che tali matrici sono simmetriche e semidefinite (o definite)
positive; inoltre queste matrici hanno gli stessi autovalori (che indicheremo
con 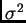 ) positivi e con la stessa molteplicità.
) positivi e con la stessa molteplicità.
Si ottengono, quindi, le seguenti rappresentazioni spettrali:
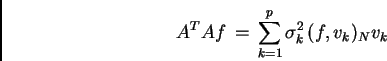 |
(A.1) |
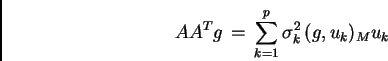 |
(A.2) |
Valgono le seguenti relazioni:
Si ottengono le seguenti rappresentazioni:
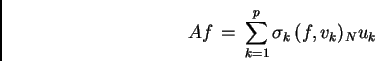 |
(A.3) |
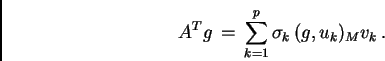 |
(A.4) |
Si ottiene, così, la decomposizione a valori singolari (SVD)
di una matrice 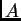 arbitraria e della sua trasposta.
arbitraria e della sua trasposta.
Sia 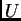 la matrice isometrica di dimensione
la matrice isometrica di dimensione 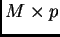 , le cui colonne sono
costituite dai vettori
, le cui colonne sono
costituite dai vettori
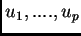 ; sia
; sia 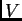 la matrice isometrica di dimensioni
la matrice isometrica di dimensioni
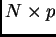 , le cui colonne sono i vettori
, le cui colonne sono i vettori
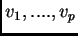 ; allora si può
scrivere:
; allora si può
scrivere:
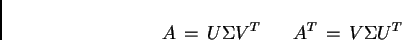 |
(A.5) |
dove 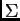 è la matrice diagonale di dimensioni
è la matrice diagonale di dimensioni 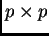 , avente gli
autovalori
, avente gli
autovalori 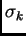 con
con 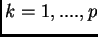 sulla diagonale principale.
sulla diagonale principale.
Se si deve risolvere il seguente sistema lineare algebrico:
dove 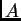 è una matrice di dimensione
è una matrice di dimensione 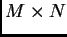 di rango
di rango 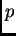 , si può trovare
la soluzione generalizzata
, si può trovare
la soluzione generalizzata 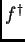 , ovvero la soluzione ai minimi quadrati
avente norma minima, tramite la SVD.
, ovvero la soluzione ai minimi quadrati
avente norma minima, tramite la SVD.
Le soluzioni ai minimi quadrati sono tutte e sole le soluzioni del seguente
problema:
Esse costituiscono le soluzioni dell'equazione di Eulero:
Dalle formule (A.1) e (A.4) si ottiene:
e quindi eguagliando le componenti secondo i 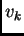 si ha:
si ha:
Quindi la soluzione generalizzata 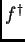 è la seguente:
è la seguente:
Essa può anche essere scritta nella seguente forma
La matrice 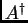 di dimensioni
di dimensioni 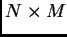 e di rango
e di rango 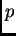 è detta
matrice inversa generalizzata (o inversa di Moore-Penrose) di
è detta
matrice inversa generalizzata (o inversa di Moore-Penrose) di 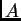 .
.
Dall'equazione (A.5 della SVD di 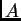 si ottiene la SVD di
si ottiene la SVD di 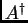 :
:




Next: Codice prodotto
Up: Algoritmi matematici utilizzati
Previous: Metoto iterativo di Landweber-Fridman
Contents
Anna Custo
2002-02-05
![]() simmetrica, di dimensioni
simmetrica, di dimensioni ![]() ,
con elementi reali tale che
,
con elementi reali tale che