Word Translation with Optimal Transport
OT-based approaches to fully unsupervised bilingual lexical induction
TL;DR: Unsupervised word translation can be cast as matching vectors across word embedding spaces. Optimal Transport is a neat, principled way to compute optimal matchings across metric domains, but it’s not directly applicable to this task (see below). We propose two approaches (this one and this one) to overcome this.
Background
Cross-lingual or cross-domain correspondences play key roles in tasks ranging from machine translation to transfer learning. Recently, purely unsupervised methods operating on monolingual embeddings have become effective alignment tools. Current state-of-the-art methods, however, involve multiple steps, including heuristic post-hoc refinement strategies. Optimal Transport provides a principled, compact and well-understood optimization approach to the problem of finding correspondences across objects. However, OT cannot be applied directly, as it assumes that the two spaces are registered, i.e., that meaningful distances can be computed across them. This is not the case for word embeddings, as they are estimated in a relative manner (based on inner products and distances), leaving, e.g., an overall rotation unspecified. To solve this challenge, we rely on two generalizations of optimal transport that allow it to operate on unregistered spaces: the Gromov-Wasserstein distances (Memoli, 2011) and a novel framework for endowing the OT objective with invariance to rotations.
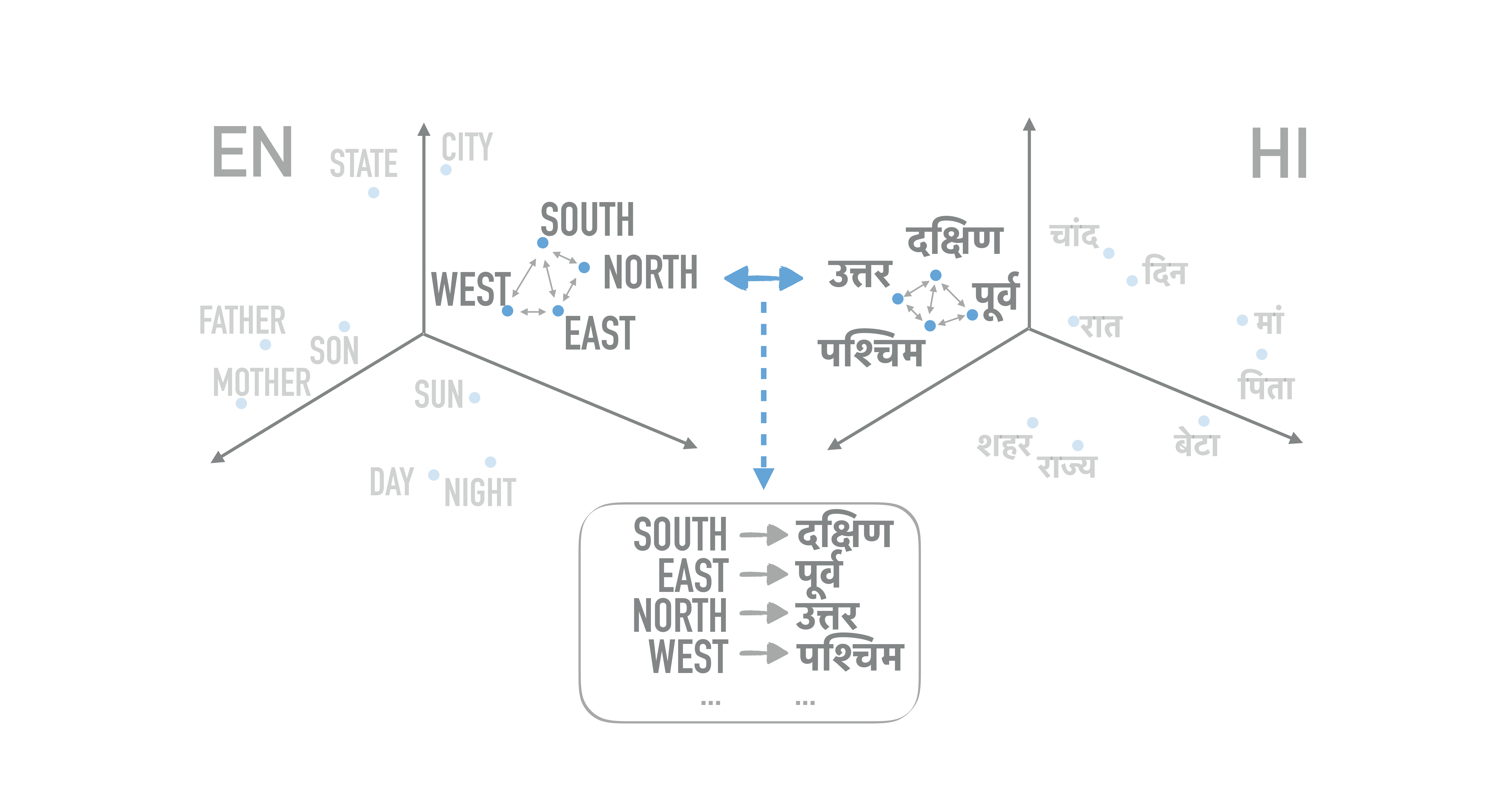
First Approach: Using the Gromov-Wasserstein Distance
The Gromov-Wasserstein distance (Mémoli, 2011) generalizes OT by directly comparing the metric spaces defined by the embeddings, instead of samples across the spaces. In other words, this framework operates on distances between pairs of points calculated within each domain and measures how these distances compare to those in the other domain. Thus, it requires a weaker but easy to define notion of distance between distances, and operates on pairs of points, turning the problem from a linear to a quadratic one.
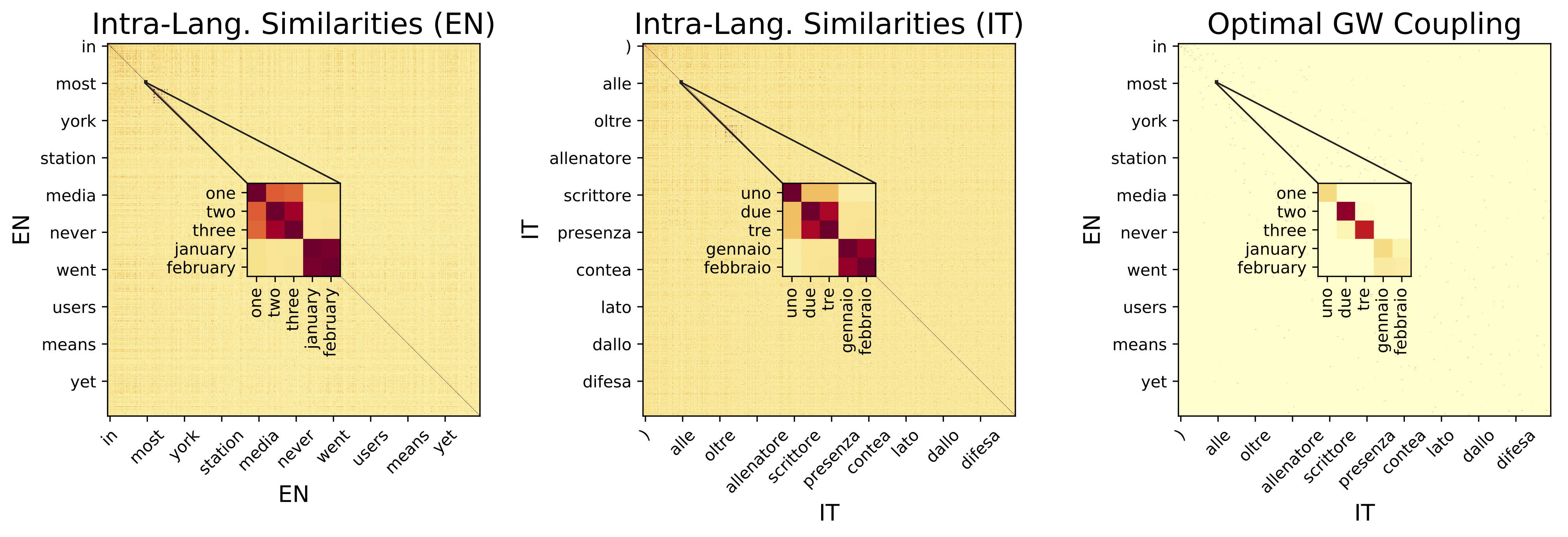
Second Approach: Using Optimal Transport with Invariances
We endow the OT objective with invariance to rotations, by using our framework of Optimal Transport with Invariances. Further details provided in that project’s page.
Relevant Publications:
- Alvarez-Melis and Jaakkola. “Gromov-Wasserstein Alignment of Word Embedding Spaces”, EMNLP 2018.
- Alvarez-Melis, Jegelka and Jaakkola. “Towards Optimal Transport with Global Invariances”, AISTATS 2019.
