Extrapolating the Limit

	http://people.csail.mit.edu/jaffer/III/Limit.html
	Extrapolating the Limit

Background

This investigation grew out of considerations in revising the specification of the algorithmic language Scheme. The designers of programming languages must deal with the corner cases 0/0 and 0⁰. Those operations being undefined in the field of Reals, the return values are often justified in terms of the limits of functions:

lim x `->` 0	x`/`x = 1		lim x `->` 0	0`/`x = 0
lim x `->` 0+	x^x = ∞		lim x `->` 0+	0^x = 0		lim x `->` 0-	0^x = ∞		lim x `->` 0	x⁰ = 1

So no single value is correct to return from 0/0 or 0⁰ in all circumstances. Some languages with multiple numeric types specify different results for zeros of different types. Constraining the behavior by numeric type is an opaque, and hence undesirable, practice.

A path which has apparently not been explored is making limit a function provided by the language.

From Wikipedia Limit of a function:

Limit of a function at a point

Suppose f is a real-valued function, then we write

lim
x -> p f(x) = L

if and only if

for every ε > 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have |f(x)-L| < ε.

Or we write

lim
x -> p f(x) = ∞

if and only if

for every R > 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) > R;

or we write

lim
x -> p f(x) = - ∞

if and only if

for every R < 0 there exists a δ > 0 such that for all real numbers x with 0 < |x-p| < δ, we have f(x) < R.

If, in the definitions, x-p is used instead of |x-p|, then we get a right-handed limit, denoted by lim_x→p+. If p-x is used, we get a left-handed limit, denoted by lim_x→p-.

These definitions are routine for analysis, with a heavy dependence on the Axiom of Choice. From a functional point of view the limit is an extrapolation of a function to a point possibly outside that function's range. From a computational point of view the first definition only allows us to check whether a given L is the limit of f(x). Because the limit doesn't always exist, we would also like our procedure to test whether the limit exists. To do this, f(x) would be evaluated at several points successively nearer to p; and the algorithm would check that the sequence of | f(x) - L | values are monotonically decreasing.

But how do we find L? The obvious approach is to evaluate f(x) at values of x near p. For maximum accuracy we would like x to be as close to p as possible. Unlike mathematical functions, floating-point functions can behave badly at points near p. To reduce the chances of f signaling an error, the goals in writing the limit algorithm are:

The range of arguments to the function f should be controlled by an input to the algorithm.
The function f should be called with values of x which are successively closer to p.
As soon as the behavior of f(x) indicates that its limit doesn't exist, the algorithm should exit without further calls to f.
The function f should not be called with argument p.

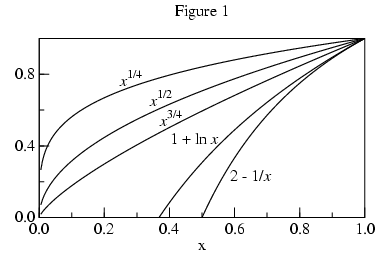One might think that the space between successive values of f(x) would decrease with x closing on p when the x are evenly spaced. But that is not necessarily the case. The square-root of 0 is 0; and that right-hand limit exists, but the square-roots near 0 are further apart than the square-roots near 1, as Figure 1 shows. In fact, the slope (1/2 x^-1/2) tends to infinity as x tends to 0.

Figure 1 also shows 1+ln(x) and 2-(1/x), functions whose limits at 0 tend to negative infinity. So how will the algorithm distinguish between vertical points-of-inflection and infinite limits? We will return to this question.

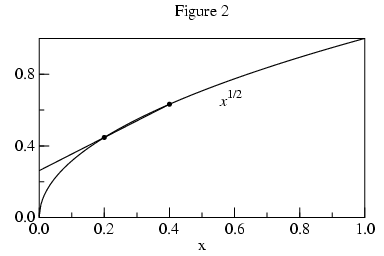curve of square root from 0 to 1 with secant pinned at x=.2 and x=.4 The central problem is how to find a value very close to f(p) without actually calling f(p). With two values of f we can construct the secant (a straight line connecting two points on a curve) and find its intersection with x=p. Using this extrapolated value will be more accurate than the value of f at the sample nearest to p.

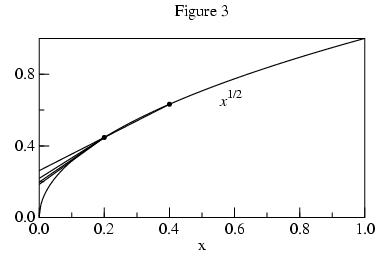
Using values of f at additional points allows us to fit higher order curves and acheive better approximations. For n+1 points we can fit f(x) to an nth order polynomial. The extrapolated L values versus n are:
curve of square root with secants having several slopes

n = 2:: 2 f1 - f2
n = 3:: 3 f1 - 3 f2 + f3
n = 4:: 4 f1 - 6 f2 + 4 f3 - f4
n = 5:: 5 f1 - 10 f2 + 10 f3 - 5 f4 + f5

The coefficient of the kth f value is

(	n	)	(-1)^k+1
	k

This polynomial extrapolation will be accurate for curves with finite slopes at the limit point p. As the tangents of figure 3 show, this extrapolation is less satisfactory when the slope at the limit point tends to infinity. Fitting a polynomial to the inverse of f would give a better estimate of f(p); in the case of roots of polynomial equations, it would yield exact results. The monotonicity conditions developed later will guarantee that the inverse function is single valued.

For n=2 the fit for the forward and inverse curves (actually lines) are the same:

e0 : g(x) := a*x + b;

g(x): g(x)

e3 : eliminate([0=g(f0), 1=g(f1), 2=g(f2)], [b, a]);

e3: 0 = f0 - 2 f1 + f2

For n=3, things get more complicated.

e4 : g(x) := a*x^2 + b*x + c;

g(x): g(x)

e4 : eliminate([0=g(f0), 1=g(f1), 2=g(f2), 3=g(f3)], [c, b, a]);

            2           2        2       2                         2        2
e4: 0 = - f0  f1 + f0 f1  + (2 f0  - 3 f1 ) f2 + (- 2 f0 + 3 f1) f2  + (- f0  + 

                           2     2                          2
                       2 f1  - f2 ) f3 + (f0 - 2 f1 + f2) f3

The value of f0(=L) which makes the equation true can be determined by a root-finder; or by solving this degree 2 polynomial in f0 using the quadratic formula.

As the degree is increased, expression size grows exponentially; quickly becoming unwieldy.

e3 : g(x) := a*x^3 + b*x^2 + c*x + d;

g(x): g(x)

e4 : eliminate([0=g(f0), 1=g(f1), 2=g(f2), 3=g(f3), 4=g(f4)], [d, c, b, a]);

                 3   2     2   3          3           3    2        2
e3:     0 = (- f0  f1  + f0  f1 ) f2 + (f0  f1 - f0 f1 ) f2  + (- f0  f1 + 

           2    3        3   2       2   3          3       3    2        2
      f0 f1 ) f2  + (2 f0  f1  - 2 f0  f1  + (- 3 f0  + 4 f1 ) f2  + (3 f0  - 

         2    3              3             3        3       3
     4 f1 ) f2 ) f3 + (- 2 f0  f1 + 2 f0 f1  + (3 f0  - 4 f1 ) f2 + (- 3 f0 + 

              3    2        2             2          2       2
      4 f1) f2 ) f3  + (2 f0  f1 - 2 f0 f1  + (- 3 f0  + 4 f1 ) f2 + (3 f0 - 

             2    3        3   2     2   3        3       3    2          2
     4 f1) f2 ) f3  + (- f0  f1  + f0  f1  + (2 f0  - 3 f1 ) f2  + (- 2 f0  + 

          2    3        3       3     3    2      2       2     2    3
      3 f1 ) f2  + (- f0  + 2 f1  - f2 ) f3  + (f0  - 2 f1  + f2 ) f3 ) f4 + 

          3           3          3       3                       3      3
       (f0  f1 - f0 f1  + (- 2 f0  + 3 f1 ) f2 + (2 f0 - 3 f1) f2  + (f0  - 

           3     3                            3    2        2           2
       2 f1  + f2 ) f3 + (- f0 + 2 f1 - f2) f3 ) f4  + (- f0  f1 + f0 f1  + 

         2       2                         2        2       2     2
    (2 f0  - 3 f1 ) f2 + (- 2 f0 + 3 f1) f2  + (- f0  + 2 f1  - f2 ) f3 + (f0 - 

                                             2    3
                                2 f1 + f2) f3 ) f4

Until a more tractable form is found, the algorithm will extrapolate from a quadratic fitted to 3 points of f^-1 when the slope tends to infinity near p.

Unfortunately, our approximation is strongly influenced by the closest f(x) sample. Using the approximation value for L in the convergence test prevents the algorithm from exiting early when the limit doesn't exist.

Although |f(x)-L| is not available, derivatives of f(x) are. Secants are proportional to the derivative of f(x). By the Mean value theorem, there is a point between the secant endpoints such that the derivative of f at that point equals the slope of the secant.

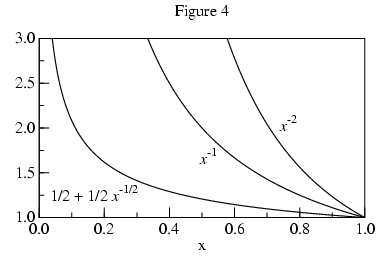family of curves of intersecting at (1,1) Approaching p, monotonic curves whose limit points tend to infinity are as steep or steeper than logarithms (hyperbolic, for example). Thus the algorithm should look for |f'(x)| increasing proportionally faster than |1/(x-p)| as x tends toward p. If that is the case, then the limit is infinite. If |f'(x)| is monotonic and increases more slowly than |1/(x-p)| as x tends toward p, then L is extrapolated and returned.

graph of x*sin(pi/x) from x=0 to x=1 The curve sin(1/x) has no limit at 0; its derivative,

-cos(1/x)
x²
, has an envelope increasing proportionally faster than |1/x| as x tends toward 0.

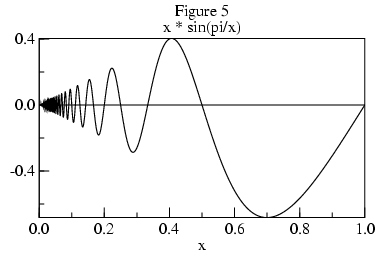
Figure 5 shows a curve of x sin(pi/x), whose limit at 0 is 0. Figure 6 shows its derivative, whose envelope is pi/x.

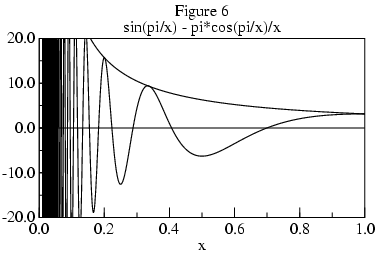
graph of sin(pi/x)-pi*cos(pi/x)/x from x=0 to x=1 and its envelope

The derivative has infinitely many peaks approaching x=0. The distance between adjacent peaks and valleys is:
x²
x - 1
The area under the derivative between adjacent zero-crossings is proportional to:
x² sin(pi/x) - x pi cos(pi/x)
x - 1
Consider the integral of this (derivative) curve as the series generated by the substitution t=1/x. Each term in the series corresponds to one peak or valley; its area proportional to
sin(pi t) - pi t cos(pi t)
t² - t
With t taking integer values, the sine term disappears and the cosine is (-1)^t:
====
\
/
==== pi (-1)^t
t - 1
Not absolutely convergent, this series meets the Cauchy criterion for conditional convergence.

While it may be possible to determine whether a limit exists from the envelope of such curves, because the magnitude of the derivative tends to infinity as x nears 0, its values are of no use in extrapolating the limit L. Apart from needing to formalize the concept of envelope, non-monotonic curves present practical problems for algorithms which will examine f at only a small number of points. If the algorithm is unlucky in its choice of points, then it will incorrectly gage the envelope. For these reasons, the algorithm is restricted to monotonic functions.

One-sided limit algorithm

Inputs:

f is a real function of one variable whose derivative is monotonic or constant over the interval p+r to p+r/n.
p is the limit point
r is the sample range width
n is an integer greater than 2

The function f should be continuously differentiable over the interval p+r to p+r/n.
It will be called up to n times with an argument in that interval.

For integer j, 0 < j < n+1, let x_j = p+(r j/n).

For 1 < j < n+1, let s_j = f(x_j) - f(x_j-1).

Let h_n = |s_n|.

For 1 < j < n, let h_j = h_n n/j.

If for 1 < j < n, |s_j| =< |s_j+1|, then the limit is extrapolated from the degree n polynomial passing through
(x_j, f(x_j)) for 0 < j < n+1.

If for 1 < j < n, |s_j| > |s_j+1| and |s_j| < h_j, then the limit is extrapolated from the quadratic passing through
(f(x₁), x₁),
(f(x₂), x₂), and
(f(x₃), x₃).

If for 1 < j < n, |s_j| > |s_j+1| and |s_j| >= h_j, then the limit tends to infinity of sign s₂.

Otherwise, the limit does not exist at scale r.

From Wikipedia Limit of a function:

Limit of function at infinity

Suppose f(x) is a real-valued function. We can also consider the limit of function f when x increases or decreases indefinitely.
We write

lim
x -> ∞ f(x) = L

if and only if

for every ε > 0 there exists S >0 such that for all real numbers x>S, we have |f(x)-L|<ε

or we write

lim
x -> ∞ f(x) = ∞

for every R > 0 there exists S >0 such that for all real numbers x>S, we have f(x)>R.

Similarly, we can define the expressions

lim
x -> ∞ f(x) = -∞

,
lim
x -> -∞ f(x) = L

,
lim
x -> -∞ f(x) = ∞

, and
lim
x -> -∞ f(x) = -∞

.

For the point limits we evaluated f at a succession of evenly spaced points leading to the limit point p. Uniform spacing doesn't lead to an infinite limit point. Instead, we transform the problem by taking a point limit of g(x)=f(1/x) at 0 from 1/r.

Praxis

The limit procedure has been coded in Scheme as part of the SLIB Scheme Library.

I am a guest and not a member of the MIT Computer Science and Artificial Intelligence Laboratory. My actions and comments do not reflect in any way on MIT.
	agj @ alum.mit.edu	Go Figure!