


Next: Condition on Angular Velocity
Up: Rendezvous Without Coordinates1
Previous: Cycle plus branches
Guaranteed Rendezvous of Agents with Bounded, Varying Speeds
In this section, we generalize the results for identical agents by removing the restriction that requires all 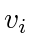 's to be identical. We say that the speed
's to be identical. We say that the speed 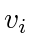 of agent
of agent  is bounded if
is bounded if
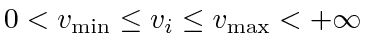 for some constants
for some constants 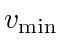 and
and 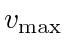 . The velocity
. The velocity 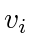 may change over time. When all agents' speeds in a pursuit are bounded, we say the pursuit is a bounded speed pursuit.
may change over time. When all agents' speeds in a pursuit are bounded, we say the pursuit is a bounded speed pursuit.
Theorem 13
Bounded speed cyclic pursuit of  Dubins car agents will rendezvous in finite time if the agents maintain their targets in the windshields of span
Dubins car agents will rendezvous in finite time if the agents maintain their targets in the windshields of span
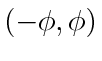 with
with
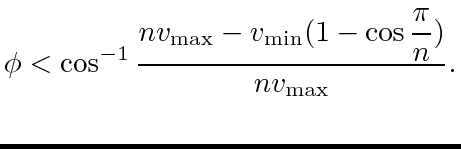 |
(32) |
PROOF. For the proof we work with (9) and use the approach in the proof of Lemma 7. The simple polygon case is covered here; the proof for the self-intersecting polygon case then follows that of Lemma 8 similarly, which we do not repeat. Let
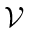 represent the agents speeds
represent the agents speeds
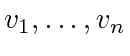 and define
and define 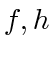 , and
, and 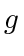 as
as
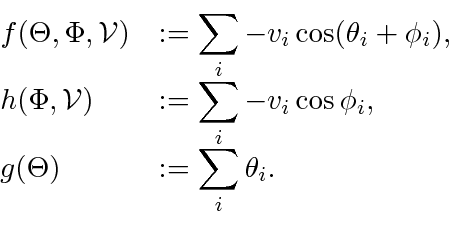 |
(33) |
The structures,
 ,
,
 , and the hyperplane
, and the hyperplane
 from Lemma 7 remain the same. For the
from Lemma 7 remain the same. For the
 slice by the hyperplane, applying the method of Lagrange multipliers to
slice by the hyperplane, applying the method of Lagrange multipliers to 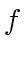 as a function of
as a function of 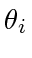 's with constraint
's with constraint
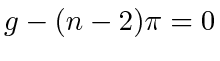 yields that for all
yields that for all  ,
,
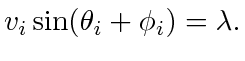 |
(34) |
Once again, holding 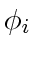 's fixed, for
's fixed, for 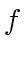 to take maximum on the
to take maximum on the
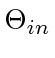 slice, for all
slice, for all  ,
,
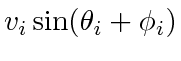 must take the same value and therefore, must be positive if we keep
must take the same value and therefore, must be positive if we keep
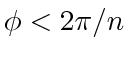 . Let us assume that we pick some
. Let us assume that we pick some
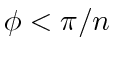 , then
, then
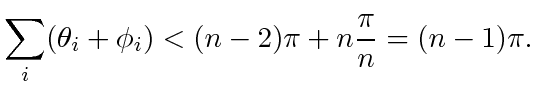 |
(35) |
By the pigeonhole principle, for at least one 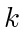 ,
,
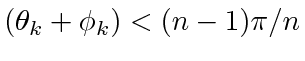 . Therefore,
. Therefore,
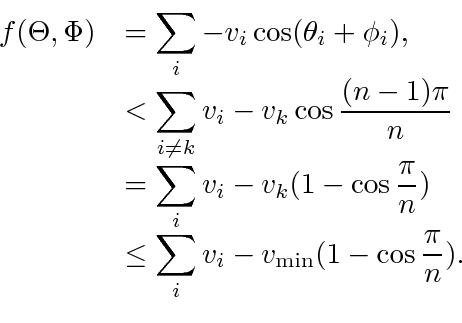 |
(36) |
To make 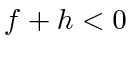 , we need
, we need 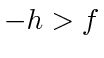 , which is true if
, which is true if
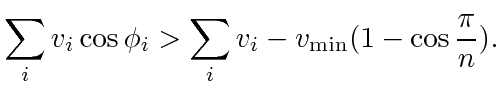 |
(37) |
One way to satisfy this is to make sure that for each  ,
,
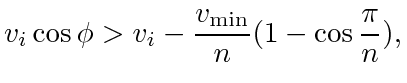 |
(38) |
or equivalently,
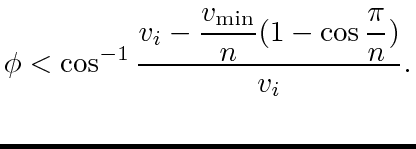 |
(39) |
The right side of (39) achieves the global minimum when
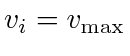 , which gives us (32) as a sufficient condition for
, which gives us (32) as a sufficient condition for
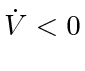 on the
on the
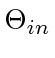 slice. On the
slice. On the
 slice, we have that
slice, we have that
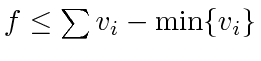 , which is less than the last expression in (36); therefore, (32) also works for the
, which is less than the last expression in (36); therefore, (32) also works for the
 slice. The finite time guarantee follows the argument from Corollary 9.
slice. The finite time guarantee follows the argument from Corollary 9.
Moving to the intree case, when agents have different speeds, no equivalent of Lemma 11 can be stated since
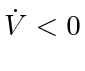 can no longer be guaranteed. A simple example is illustrated in Fig. 5. Agent
can no longer be guaranteed. A simple example is illustrated in Fig. 5. Agent 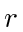 is at the root and does not move. Suppose agent
is at the root and does not move. Suppose agent  moves very fast and agents (
moves very fast and agents (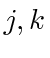 in the figure) following
in the figure) following  barely move. Also assume that all agents are almost colinear. It is straightforward to see that, after a short period of time (the second drawing), the sum of the length of all edges, or
barely move. Also assume that all agents are almost colinear. It is straightforward to see that, after a short period of time (the second drawing), the sum of the length of all edges, or 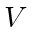 , increases. This suggests that
, increases. This suggests that 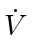 must be positive at some point. However, such a system will still rendezvous. Supposing that the stationary agent is
must be positive at some point. However, such a system will still rendezvous. Supposing that the stationary agent is 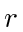 , at least one agent, say
, at least one agent, say  , is assigned to
, is assigned to 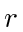 . Thus,
. Thus,
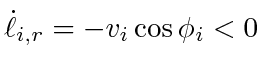 whenever
whenever
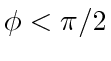 . Hence, agent
. Hence, agent  will merge into agent
will merge into agent 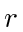 in finite time, and all other agents will eventually follow. We have proved:
in finite time, and all other agents will eventually follow. We have proved:
Lemma 14
Bounded speed pursuit of  Dubins car agents with an intree assignment graph will merge into the stationary agent in finite time if the agents maintain their targets in the windshields of span
Dubins car agents with an intree assignment graph will merge into the stationary agent in finite time if the agents maintain their targets in the windshields of span
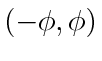 with
with
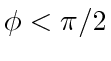 .
.
Figure 5:
Bounded speed intree pursuit may not have 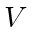 dot less than zero at all times.
dot less than zero at all times.
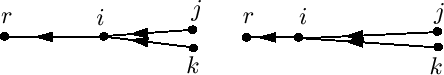 |
Since it is not possible to guarantee
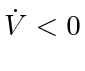 at all times for the bounded speed case, a result like Theorem 12 is out of the question. However, since Theorem 13 and Lemma 14 parallel Theorem 4 and Lemma 11, the argument giving us sequential rendezvous in the identical agents case continues to hold:
at all times for the bounded speed case, a result like Theorem 12 is out of the question. However, since Theorem 13 and Lemma 14 parallel Theorem 4 and Lemma 11, the argument giving us sequential rendezvous in the identical agents case continues to hold:
Theorem 15
Bounded speed pursuit of  Dubins car agents with arbitrary connected, single-target assignment graph will rendezvous in finite time if the agents maintain their targets in the windshields of span
Dubins car agents with arbitrary connected, single-target assignment graph will rendezvous in finite time if the agents maintain their targets in the windshields of span
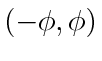 with fixed
with fixed 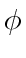 satisfying (32).
satisfying (32).



Next: Condition on Angular Velocity
Up: Rendezvous Without Coordinates1
Previous: Cycle plus branches
Jingjin Yu
2011-01-18
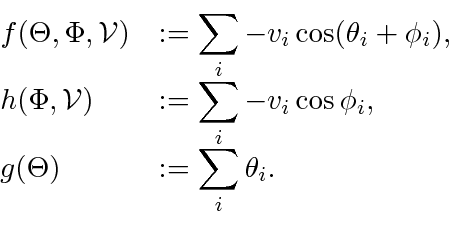
![]() can no longer be guaranteed. A simple example is illustrated in Fig. 5. Agent
can no longer be guaranteed. A simple example is illustrated in Fig. 5. Agent ![]() is at the root and does not move. Suppose agent
is at the root and does not move. Suppose agent ![]() moves very fast and agents (
moves very fast and agents (![]() in the figure) following
in the figure) following ![]() barely move. Also assume that all agents are almost colinear. It is straightforward to see that, after a short period of time (the second drawing), the sum of the length of all edges, or
barely move. Also assume that all agents are almost colinear. It is straightforward to see that, after a short period of time (the second drawing), the sum of the length of all edges, or ![]() , increases. This suggests that
, increases. This suggests that ![]() must be positive at some point. However, such a system will still rendezvous. Supposing that the stationary agent is
must be positive at some point. However, such a system will still rendezvous. Supposing that the stationary agent is ![]() , at least one agent, say
, at least one agent, say ![]() , is assigned to
, is assigned to ![]() . Thus,
. Thus,
![]() whenever
whenever
![]() . Hence, agent
. Hence, agent ![]() will merge into agent
will merge into agent ![]() in finite time, and all other agents will eventually follow. We have proved:
in finite time, and all other agents will eventually follow. We have proved:
![]() at all times for the bounded speed case, a result like Theorem 12 is out of the question. However, since Theorem 13 and Lemma 14 parallel Theorem 4 and Lemma 11, the argument giving us sequential rendezvous in the identical agents case continues to hold:
at all times for the bounded speed case, a result like Theorem 12 is out of the question. However, since Theorem 13 and Lemma 14 parallel Theorem 4 and Lemma 11, the argument giving us sequential rendezvous in the identical agents case continues to hold: