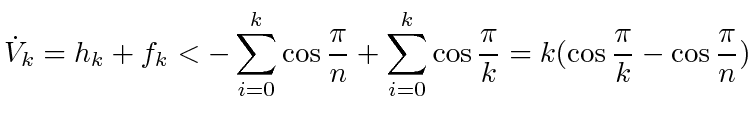Next: Guaranteed Rendezvous of Agents
Up: Guaranteed Rendezvous of Identical
Previous: The intree case
Given an arbitrary connected, single-target assignment graph with a cycle plus some branches, Theorem 4 and Lemma 11 ensure that the whole system will rendezvous in a sequential manner: First, the agents on the cycle will rendezvous and merge into a single stationary agent. The rest of the agents will then merge into the stationary agent. We call this type of rendezvous sequential rendezvous. So far, however, there is no guarantee that the entire system has
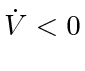 all the time. Therefore, no equivalent of Proposition 10 can be stated for an arbitrary connected, single-target assignment graph yet, which means that such a system may not be stable in the sense of Lyapunov. In this subsection we show that it is possible to guarantee
all the time. Therefore, no equivalent of Proposition 10 can be stated for an arbitrary connected, single-target assignment graph yet, which means that such a system may not be stable in the sense of Lyapunov. In this subsection we show that it is possible to guarantee
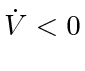 at all times for identical agents.
at all times for identical agents.
PROOF. We only need to show that
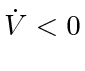 always holds under the condition (27), the same arguments from Corollary 9 and Proposition 10 then give us the rest. Lemma 8 and Lemma 11 cover the single cycle and intree assignment graphs, which leaves only the case of a cycle plus some branches (see Fig. 3). For any connected, single-target assignment graph with
always holds under the condition (27), the same arguments from Corollary 9 and Proposition 10 then give us the rest. Lemma 8 and Lemma 11 cover the single cycle and intree assignment graphs, which leaves only the case of a cycle plus some branches (see Fig. 3). For any connected, single-target assignment graph with  agents, there is a single cycle. Assume that there are
agents, there is a single cycle. Assume that there are 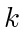 agents on that cycle. Let
agents on that cycle. Let 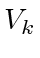 denote the corresponding Lyapunov function for the
denote the corresponding Lyapunov function for the 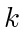 -cycle and let
-cycle and let
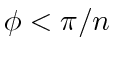 . Then for the agents on the cycle,
. Then for the agents on the cycle,
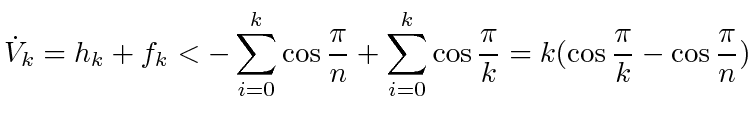 |
(28) |
holds for 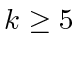 . Here
. Here 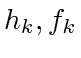 are defined similarly as
are defined similarly as 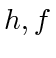 before. For the agents not on the cycle, we have
before. For the agents not on the cycle, we have
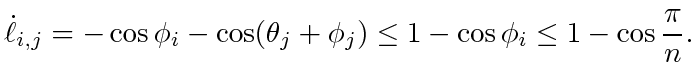 |
(29) |
Summing up all the terms for the cycle plus 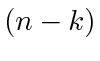 other agents not on that cycle, we have
other agents not on that cycle, we have
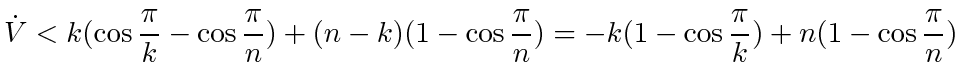 |
(30) |
We want to show that the right hand side above is negative at all times. We may do this by showing that the function,
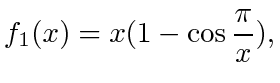 |
(31) |
decreases monotonically for
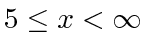 . This can be verified by showing that
. This can be verified by showing that
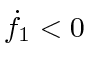 on the domain.
When
on the domain.
When
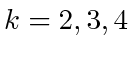 ,
, 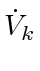 is less than
is less than 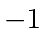 by direct computation; hand checking shows that
by direct computation; hand checking shows that
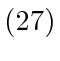 guarantees
guarantees
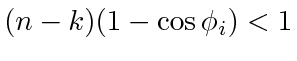 , which in turn guarantees
, which in turn guarantees
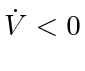 .
.



Next: Guaranteed Rendezvous of Agents
Up: Guaranteed Rendezvous of Identical
Previous: The intree case
Jingjin Yu
2011-01-18