


Next: Bibliography
Up: Rendezvous Without Coordinates1
Previous: Appendix B: Remaining Proofs
If the windshield of an agent is a single point (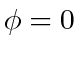 ), every agent moves directly toward its target, and we obtain a version of the classic cyclic pursuit, or
), every agent moves directly toward its target, and we obtain a version of the classic cyclic pursuit, or  -bug problem. We call this variety the direct cyclic pursuit problem to distinguish it from the Dubins car cyclic pursuit. If we are not sure whether such pursuit is cyclic, we call it direct pursuit. Such cases can be viewed as limiting cases as the windshield goes from an open interval to a point. Here we show that our approach also applies to this special case. Allowing the pursuit formation to be an arbitrary polygon and using the general form of
-bug problem. We call this variety the direct cyclic pursuit problem to distinguish it from the Dubins car cyclic pursuit. If we are not sure whether such pursuit is cyclic, we call it direct pursuit. Such cases can be viewed as limiting cases as the windshield goes from an open interval to a point. Here we show that our approach also applies to this special case. Allowing the pursuit formation to be an arbitrary polygon and using the general form of 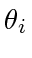 defined for self-intersecting polygon, (9) becomes:
defined for self-intersecting polygon, (9) becomes:
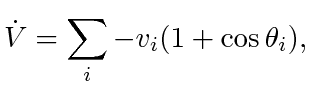 |
(51) |
with
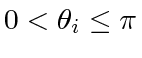 and
and
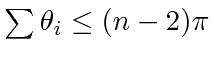 . Since for at least one
. Since for at least one  ,
,
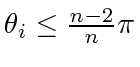 ,
,  is always strictly negative for fixed
is always strictly negative for fixed  and any set of
and any set of
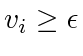 for some fixed
for some fixed
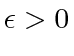 . The intree and cycle plus branch cases also follow. We obtain the following corollary:
. The intree and cycle plus branch cases also follow. We obtain the following corollary:
Corollary 19
Direct pursuit of  agents with lower bounded speed and arbitrary connected, single-target assignment graph will rendezvous in finite time.
agents with lower bounded speed and arbitrary connected, single-target assignment graph will rendezvous in finite time.
We can say a little more if 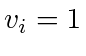 (or any constant) holds for all agents:
(or any constant) holds for all agents:
PROOF. Writing
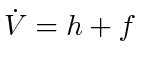 as that of (13), we readily see that
as that of (13), we readily see that 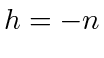 for such systems. (52) is then easily obtained by substituting in (22).
for such systems. (52) is then easily obtained by substituting in (22).



Next: Bibliography
Up: Rendezvous Without Coordinates1
Previous: Appendix B: Remaining Proofs
Jingjin Yu
2011-01-18